Ανίχνευση γραμμικών χαρακτηριστικών χρησιμοποιώντας πολλαπλής ανάλυσης κυματιδιακά φίλτρα
Από RemoteSensing Wiki
Ανίχνευση γραμμικών χαρακτηριστικών χρησιμοποιώντας πολλαπλής ανάλυσης κυματιδιακά φίλτρα
Πρωτότυπος τίτλος : Lineal Feature Detection Using
Multi-resolution Wavelet Filters.Πηγή : Samuel P. Kozaitis and R.H. Cofer, Photogrammetric Engineering & Remote Sensing
Vol. 71, No. 6, June 2005, pp. 689–697.
[4]
<b>Περίληψη
Σε αυτό το έγγραφο, ανιχνεύονται οδικά pixels σε εναέριες φωτογραφίες χρησιμοποιώντας μια πολλαπλής-ανάλυσης κυματιδιακή προσέγγιση. Η μέθοδος περιλαμβάνει μια διαφορική γεωμετρική προσέγγιση για την ανίχνευση των pixels που αποτελούν οδικό δίκτυο βάσει των μετατροπών των κυματιδίων. Χρησιμοποιώντας τη προσέγγιση αυτή, μας επιτρέπει να επεκτείνουμε τη διαφορική προσέγγιση γεωμετρίας προκειμένου να ενσωματώσει τις πολλαπλές κλίμακες. Οι γραμμικοί αλγόριθμοι ανίχνευσης χαρακτηριστικών γνωρισμάτων είναι ευαίσθητοι στις αλλαγές των εικόνων. Επομένως, απαιτείται μια μέθοδος ισχυρή στις παραλλαγές των εικόνων κι έτσι θα βελτιωνόταν η πιθανότητα της επιτυχίας της επόμενης επεξεργασίας. Η μετατροπή των κυματιδίων αποτλεί μια κατάλληλη μέθοδο για τις πληροφορίες στις διαφορετικές αναλύσεις εικόνας. Παραδείγματος χάριν, έχει αποδειχθεί ότι η εξέλιξη των τοπικών μεγίστων κυματιδίων στις κλίμακες χαρακτηρίζει την τοπική μορφή των δομών. Λόγω του ότι οι ιδιομορφίες μπορούν να εμφανιστούν σε όλες τις κλίμακες, οι μετατροπές κυματιδίων πολλαπλών-κλιμάκων έχουν χρησιμοποιηθεί για να ανιχνεύσουν τις ακμές, τα όρια και τους δρόμους. Έχει αποδειχθεί ότι τα προϊόντα των συντελεστών πολλαπλών-κλιμάκων της μετατροπής κυματιδίων μειώνουν γενικά το συσχετισμό του εισαγώμενου θορύβου διότι έχουν μια έμφυτη δυνατότητα να καταστείλουν τις απομονωμένες ωθήσεις και τους στενούς σφυγμούς, ανάλογα με το ποσό της χρησιμοποιούμενης λείανσης. Επιπλέον,έχει αναπτυχθεί μια ισχυρή μέθοδος για την ανίχνευση ακμών για τις θορυβώδεις εικόνες, χρησιμοποιώντας τα προϊόντα της μετατροπής κυματιδίων στις κλίμακες. Εξετάστηκε μια διαφορική προσέγγιση γεωμετρίας για την ανίχνευση των οδικών pixels σε ενιαία κλίμακα. Σε αυτή τη προσέγγιση, χρησιμοποιήθηκαν για να ανιχνεύσουν τα pixels των γραμμών οι μεγάλες τιμές της απόλυτης αξίας του δεύτερου παραγώγου κατεύθυνσης μιας εικόνας, η χρησιμοποίηση ενός δεύτερου παραγώγου ενός γκαουσσιανού φίλτρου [5] και η εξαφάνιση των πρώτων παραγώγων κατεύθυνσης σε μια κανονική κατεύθυνση . Αναδιατυπώθηκε αυτή η προσέγγιση στα πλαίσια ενός συνεχούς πλαισίου κυματιδίων έτσι ώστε να μπορούμε να χρησιμοποιήσουμε μια αντίστοιχη πρσέγγιση για την οδική ανίχνευση. Χρησιμοποιήθηκε αυτή η διαφορική προσέγγιση γεωμετρίας πολλαπλών-κλιμάκων για να παραχθούν τα χωρικά φίλτρα περιοχών για την εξαγωγή οδικών pixels. Ένας ανθρώπινος χειριστής προτείνει την υπόθεση ότι μεταξύ δύο σημείων υπάρχει δρόμος. Κατόπιν, ο υπολογιστής εκτελεί το χαμηλού επιπέδου στόχο από την εύρεση των οδικών pixels. Σε αυτήν την προσέγγιση, απαιτείται μια υψηλής-πιθανότητας μέθοδος που ανιχνεύει τα χαρακτηριστικά γνωρίσματα, όπως τα pixels οδικού δικτύου. Έπειτα, εξετάζεται η θεωρία πίσω από τη προσέγγισή αυτή και συγκρίνει τα αποτελέσματα της προσέγγισης πολλαπλής-κλίμακάς με αυτή μιας ενιαίας κλίμακας και έπειτα επικυρώνεται με τη χρήση συνθετικών εικόνων.
Μεθοδολογία
Προσπαθώντας να αξιολογηθεί η προτεινόμενη μέθοδος, εφαρμόστηκαν τα πειράματα σε συνθετικές εικόνες με αρκετές διαβαθμίσεις θορύβου. Χρησιμοποιήσαμε δύο εικόνες, όπου κάθε μια αποτελείται από μια ενιαία περιοχή κύκλων διαμέτρου 147 pixels, και το πλάτος τους είναι ένα και επτά pixels αντίστοιχα, σε ένα σταθερό (μηδέν) υπόβαθρο. Χρησιμοποιήσαμε τις εικόνες των κύκλων για να διατηρηθούν αμετάβλητες όλες οι γωνίες ενός δρόμου. Ποικίλαμε την αναλογία (SNR) των συνθετικών εικόνων χρησιμοποιώντας τον πρόσθετο γκαουσσιανό λευκό θόρυβο. Μετά από την επεξεργασία των συνθετικών εικόνων που χρησιμοποιούν τον αλγόριθμό μας, συγκρίναμε τα αποτελέσματα με μια αναφορά. Χρησιμοποιήσαμε ένα μοναδικό pixel απαλαγμένο από θόρυβο πλάτος κύκλου(???) επειδή είναι το ιδανικό αποτέλεσμα. Βρέθηκε το μέσο τετραγωνικό σφάλμα (MSE) μεταξύ της αναφοράς και των εικόνων που υποβάλονται σε επεξεργασία από τον αλγόριθμό μας ώστε να δώσει μια γενική ιδέα για την απόδοση της μεθόδου παρουσία του θορύβου. Αρχικά, υπολογίσαμε το MSE στην περιοχή που καταλήφθηκε μόνο από την περιοχή των κύκλων στην εικόνα αναφοράς και στην αντίστοιχη περιοχή στις επεξεργασμένες εικόνες. Ο υπολογισμός του MSE σε αυτή τη περιοχή έδωσε μια ένδειξη μη-εντοπισμένων οδικών εικονοκυττάρων ή λανθασμένα-εντοπισμένων. Υπολογίσαμε επίσης το MSE στην περιοχή του κύκλου στην εικόνα αναφοράς και την αντίστοιχη περιοχή στις επεξεργασμένες εικόνες.
Ο υπολογισμός του MSE σε αυτήν την περιοχή έδωσε την ένδειξη των ανιχνευμένων οδικών εικονοκυττάρων όταν δεν ήταν εκεί κανένα, or false positives. Συγκρήθηκαν τα αποτελέσματα της επεξεργασίας των δύο κλιμάκων με αυτές της μίας κλίμακας. Στην πολλαπλή κλίμακα χρησιμοποιήσαμε αυτή που χρησιμοποιήθηκε στην ενιαία κλίμακα a0 και 1.5a0.

Τα αποτελέσματα έδειξαν ότι το σφάλμα στην πολλαπλή κλίμακα ήταν το μισό σε σύγκριση με αυτό της ενιαίας κλίμακας με τη διαφορά ότι αυξάνεται όπου to SNR μειώνεται. Οπτικά, οι διαφορές μεταξύ της ενιαίος-κλίμακας και των προσεγγίσεων πολλαπλής-κλίμακας παρουσιάζονται στο σχήμα 8, όπου μια δορυφορική εικόνα 256x256 pixels χρησιμοποιήθηκαν στα πειράματα. Το αποτέλεσμα της επεξεργασίας που χρησιμοποιεί μόνο μια κλίμακα για τρίαεικονοκύτταρα δρόμων, a0 = 6, φαίνονται στο figure 8b καθώς και των δύο κλιμάκων (ao=6, ao=9). Yπολογίσαμε το MSE μεταξύ των εικόνων 8b και 8c, και το προϊόν ενός σχεδιασμένου με το χέρι οδικού δικτύου και της αρχικής εικόνας. το ΜSE της εικόνας 8c ήταν 6.2 % λιγότερο από αυτό της 8b. Όταν εξετάζονται μόνο τα pixels που αφορούν οδικό δίκτυο, το MSE αυξάνεται κατά 8% όταν επεξεργάζεται με τις πολλαπλές κλίμακες. Εντούτοις, κατά την εξέταση μη οδικού δικτύου εικονοκύτταρα, το MSE μειώθηκαν από 34.7% όταν χρησιμοποιήθηκαν οι πολλαπλάσιες κλίμακες.
Αποτελέσματα Οδικού Δικτύου
Καταφέραμε να εντοπίζουμε οδικά δίκτυα χρησιμοποιώντας προσεγγίσεις μέσω υπολογιστή. Για να ανιχνευθεί ένας δρόμος χρησιμοποιώντας αυτή τη πρσέγγιση , ένας χρήστης «βουρτσίζει» μια πορεία μεταξύ των εικονοκυττάρων έναρξης και λήξης που βρίσκονται σε ένα γραμμικό χαρακτηριστικό γνώρισμα. Το βήμα βουρτσίσματος μπορεί να γίνει πολύ γρήγορα χρησιμοποιώντας ένα εργαλείο-στυλό το πλάτος του οποίου μπορεί να ρυθμιστεί. Κατόπιν, ένας δυναμικός προγραμματιστικός αλγόριθμος λειτουργεί μόνο στη βουρτσισμένη περιοχή για να βρεί την πορεία που αποτελείται από το επιθυμητό χαρακτηριστικό γνώρισμα μεταξύ των εικονοκυττάρων έναρξης και λήξης. Η βουρτσισμένη εικόνα παρουσιάζεται στην εικόνα 9α όπου τονίζεται η ΄βουρτσισμένη΄περιοχή.

Ο δυναμικός προγραμματισμός του αλγορίθμου λειτουργεί πραγματικά στο αποτέλεσμα ανίχνευσης οδικού εικονοκυττάρου. Ουσιαστικά ο αλγόριθμος ορίζει την πιθανότητα ενός εικονοκυττάρου να είναι μέρος του δρόμου. Οι μέθοδοι προγραμματισμού για τις κοντινότερες-πορείες μεταξύ δύο εικονοκυττάρων είναι πολύ επιτυχείς στην ανίχνευση μεγάλων χαρακτηριστικών γνωρισμάτων των γραμμών στις εικόνες. Αλγόριθμοι με δυνατές προγραμματιστικές ικανότητες είναι αποί στο να τους προγραμματίσεις και είναι ιδιαίτερα αποδοτικοί, χαρακτηριστικά που το καθιστούν ικανό για τον εντοπισμό της βέλτιστης συνολικής πορείας. Ο αλγόριθμος του Dijkstra λύνει το πρόβλημα της κοντινότερης πορείας από ένα σημείο μιας γραφικής παράστασης σε έναν προορισμό. Πραγματικά, οι κοντινότερες πορείες από μια δεδομένη πηγή σε όλα τα σημεία μιας γραφικής παράστασης βρίσκονται συγχρόνως και αυτό σχετίζεται με το πρόβλημα της παρουσίας δέντρων. Η γραφική παράσταση που αντιπροσωπεύει όλες τις πορείες από μία κορυφή σε όλες τις άλλες πρέπει να είναι μια μέτρηση δέντρου,πρέπει να περιλάβει όλες τις κορυφές. Δεν θα υπάρξει επίσης κανένας κύκλος, καθότι ο κύκλος θα καθόριζε περισσότερες από μια πορείες από επιλεγμένη κορυφή τουλάχιστον σε μία άλλη κορυφή. (Περισσότερες πληροφορίες για την εφαρμογή του αλγορίθμου Dijkstra θα βρείτε εδω: http://www.asprs.org/publications/pers/2005journal/june/2005_june_689-697.pdf) Όσο χρησιμοποιούμε το περιβάλλον του υπολογιστή μας, γνωρίζουμε τη γενική θέση των εικονοκυττάρων του οδικού δικτύου και θέλουμε να τη προσδιορίσουμε χωρίς σφάλμα. Πιό χρήσιμος μιας μέτρησης είναι το μήκος ενός δρόμου που μπορεί να σχεδιαστεί σωστά. Τα εικονοκύτταρα με τις τιμές που παρεκκλίνουν από το ιδανικό αποτέλεσμα μπορεί να κοντύνουν το μήκος του δρόμου που μπορεί σχεδιαστεί.
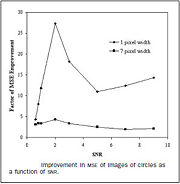
Επομένως, χρησιμοποιήσαμε το MSE ως μέτρο. Βρήκαμε ότι η αναλογία του συνολικού MSE για την πολλαπλή κλίμακα και τα αποτελέσματα της ενιαίας κλίμακας επιδεικνύουν τα αποτελέσματα στο σχήμα 10 σαν λειτουργία των SNR. Αυτά τα αποτελέσματα δίνουν μια ένδειξη αύξησης στο μήκος του δρόμου που μπορεί να αποτυπωθεί. Τα αποτελέσματα δείχνουν ότι η προσέγγισή μας αυξάνει το μήκος για τους δρόμους ενός και επτά εικονοκυττάρων ευρέως.
Συμπεράσματα
Η ομαλοποίηση των φίλτρων σε μια διαφορική προσέγγιση γεωμετρίας τους επιτρέπει να χρησιμοποιηθεί σε ένα πλαίσιο κυματιδίων. Κατά αυτόν τον τρόπο, επεκτείναμε μια διαφορική προσέγγιση γεωμετρίας που χρησιμοποιήθηκε για την ανίχνευση εικονοκυττάρων οδικού δικτύου στις πολλαπλές κλίμακες. Αυτό οδήγησε σε μια βελτίωση στην ανίχνευση των εικονοκυττάρων οδικού δικτύου. Διαπιστώσαμε ότι η χρησιμοποίηση των πολλαπλάσιων κλιμάκων μείωσε σημαντικά τον αριθμό πιθανών ψεύτικων θετικών. Η προσέγγιση λειτούργησε καλά με μια υπολογιστική προσέγγιση, όπου ο σπόρος η τα πιθανά εικονοκύτταρα που μας ενδιαφέρουν θα πρέπει να έχουν ένα υψηλό επίπεδο εμπιστοσύνης ώστε να είναι σωστό. Διαπιστώσαμε ότι η προσέγγισή μας οδήγησε σε μια αποτελεσματική μέθοδο για τους δρόμους στα εναέριες εικόνες.