Αυτόματη ανάλυση της κάλυψης εδάφους για την Τενερίφη με Επιβλεπόμενη Ταξινόμηση χρησιμοποιώντας τηλεπισκοπικά δεδομένα
Από RemoteSensing Wiki
| Γραμμή 23: | Γραμμή 23: | ||
<b>Περιοχή Μελέτης - Μέθοδοι</b><br> | <b>Περιοχή Μελέτης - Μέθοδοι</b><br> | ||
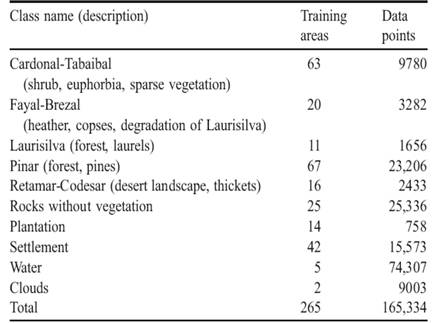
| - | Η περιοχή μελέτης για την αυτόματη ανάλυση της κάλυψης εδάφους είναι η Τενερίφη, με περίπου 2050 km2 το μεγαλύτερο από τα Κανάρια Νησιά. Λόγω της κάθετης και οριζόντιας έκτασής του καθώς και της θέσης του στη μέση του Ατλαντικού, το κλίμα της Τενερίφης και η βλάστηση ποικίλλουν έντονα. Λόγω της ετερογενούς φυσικής και καλλιεργήσιμης έκτασης, πολλές διαφορετικές τάξεις εδαφοκάλυψης έπρεπε να ληφθούν υπόψη. Από τη μια πλευρά οι τάξεις που προκύπτουν από τις μη επιβλεπόμενες ταξινομήσεις (ανάλυση συσσωρεύσεων), και από την άλλη πλευρά αυτές που προκύπτουν από τους επίγειους ελέγχους. Εξαιτίας της χονδροειδούς ανάλυσης των δορυφορικών εικόνων και του υψηλού αριθμού διαφορετικών τάξεων κάλυψης εδάφους, ήταν αναπόφευκτο να μειωθεί αυτός ο αριθμός με την τοποθέτηση των παρόμοιων τάξεων μαζί. Τελικά, αφού έγιναν όλες οι τεχνικές και γεωγραφικές εκτιμήσεις για την επιλογή των τάξεων, αποφασίσαμε να χρησιμοποιήσουμε m= 10 τάξεις στην αυτόματη ανάλυση της κάλυψης εδάφους για την Τενερίφη (πίνακας 1).<br> | + | Η περιοχή μελέτης για την αυτόματη ανάλυση της κάλυψης εδάφους είναι η Τενερίφη, με περίπου 2050 km2 το μεγαλύτερο από τα Κανάρια Νησιά. Λόγω της κάθετης και οριζόντιας έκτασής του καθώς και της θέσης του στη μέση του Ατλαντικού, το κλίμα της Τενερίφης και η βλάστηση ποικίλλουν έντονα. Λόγω της ετερογενούς φυσικής και καλλιεργήσιμης έκτασης, πολλές διαφορετικές τάξεις εδαφοκάλυψης έπρεπε να ληφθούν υπόψη. Από τη μια πλευρά οι τάξεις που προκύπτουν από τις μη επιβλεπόμενες ταξινομήσεις (ανάλυση συσσωρεύσεων), και από την άλλη πλευρά αυτές που προκύπτουν από τους επίγειους ελέγχους. Εξαιτίας της χονδροειδούς ανάλυσης των δορυφορικών εικόνων και του υψηλού αριθμού διαφορετικών τάξεων κάλυψης εδάφους, ήταν αναπόφευκτο να μειωθεί αυτός ο αριθμός με την τοποθέτηση των παρόμοιων τάξεων μαζί. Τελικά, αφού έγιναν όλες οι τεχνικές και γεωγραφικές εκτιμήσεις για την επιλογή των τάξεων, αποφασίσαμε να χρησιμοποιήσουμε m= 10 τάξεις στην αυτόματη ανάλυση της κάλυψης εδάφους για την Τενερίφη (πίνακας 1).<br><br> |
| - | [[Εικόνα:Stlas_tener_1_05.jpg|center|image|]]<i>Πίνακας 1 : Ο αριθμός των περιοχών εκπαίδευσης και ο αντίστοιχος αριθμός των δειγμάτων των σημειακών δεδομένων για τις 10 διαφορετικές τάξεις κάλυψης του εδάφους που χρησιμοποιήθηκαν στην παρούσα μελέτη.[http://www.sciencedirect.com/science/article/pii/S0034425703001305]πηγή]]</i><br> | + | [[Εικόνα:Stlas_tener_1_05.jpg|center|image|]]<i>Πίνακας 1 : Ο αριθμός των περιοχών εκπαίδευσης και ο αντίστοιχος αριθμός των δειγμάτων των σημειακών δεδομένων για τις 10 διαφορετικές τάξεις κάλυψης του εδάφους που χρησιμοποιήθηκαν στην παρούσα μελέτη.[http://www.sciencedirect.com/science/article/pii/S0034425703001305]πηγή]]</i><br><br> |
Οι δορυφορικές εικόνες που χρησιμοποιήθηκαν σε αυτή τη μελέτη είχαν ληφθεί στις 7 Αυγούστου 1988 από τον Landsat 5 ΤΜ. Επίσης ήταν χρήσιμο να χρησιμοποιήσουμε ένα Ψηφιακό Μοντέλο Υψομέτρων DEM για την κωδικοποίηση των υψομετρικών δεδομένων, έτσι ώστε να μπορεί να ενσωματωθεί στη διαδικασία της ταξινόμησης αργότερα. Στην εικόνα Landsat TM της Τενερίφης που μας δόθηκε, κάποιο μέρος του νησιού δυστυχώς καλύπτεται από σύννεφο. Για να μην έχουμε αρνητική επίδραση κατά τη ταξινόμηση, αυτά τα σύννεφα απομακρύνθηκαν εκ των προτέρων από τα κανάλια εισόδου. | Οι δορυφορικές εικόνες που χρησιμοποιήθηκαν σε αυτή τη μελέτη είχαν ληφθεί στις 7 Αυγούστου 1988 από τον Landsat 5 ΤΜ. Επίσης ήταν χρήσιμο να χρησιμοποιήσουμε ένα Ψηφιακό Μοντέλο Υψομέτρων DEM για την κωδικοποίηση των υψομετρικών δεδομένων, έτσι ώστε να μπορεί να ενσωματωθεί στη διαδικασία της ταξινόμησης αργότερα. Στην εικόνα Landsat TM της Τενερίφης που μας δόθηκε, κάποιο μέρος του νησιού δυστυχώς καλύπτεται από σύννεφο. Για να μην έχουμε αρνητική επίδραση κατά τη ταξινόμηση, αυτά τα σύννεφα απομακρύνθηκαν εκ των προτέρων από τα κανάλια εισόδου. | ||
Εξαιτίας του έντονου ανάγλυφου της Τενερίφης οι τιμές της φασματικής ανάκλασης για μια τάξη μπορεί να ποικίλλουν σημαντικά ανάλογα με την γωνία του εισερχόμενος φωτός. Ως εκ τούτου, χρησιμοποιήσαμε ακόμη μια ραδιομετρική διαδικασία διόρθωσης για να μειώσουμε την επίδραση της τοπογραφίας. Πριν ξεκινήσουμε την επιβλεπόμενη ταξινόμηση αρχικά εκτελέσαμε μια μη επιβλεπόμενη συσσώρευση για την κάθε τάξη των δεδομένων εκπαίδευσης για την ανίχνευση υποτάξεων οι οποίες θα έπρεπε να αντιμετωπιστούν ξεχωριστά. Η μέθοδος της μη επιβλεπόμενης ταξινόμησης που χρησιμοποιήσαμε για αυτό τον σκοπό είναι η μέση τεχνική μετατόπισης που αναπτύχθηκε από τους Comaniciu και Meer (2002). Το αποτέλεσμα της συσσώρευσης ορίζει ένα νέο αριθμό (μεγαλύτερο από m=10) τάξεων στα υπάρχοντα σημεία εκπαίδευσης, οι οποίες μετά χρησιμοποιούνται ως στοιχεία εισόδου στις μεθόδους επιβλεπόμενης ταξινόμησης. Τέλος, λαμβάνουμε μια κατάτμηση της εικόνας στις 10 τάξεις που καθορίστηκαν προηγουμένως, ξανασημειώνοντας κάθε pixel σε κείνη την τάξη από την οποία η ετικέτα υπό-τάξης της προήλθε. | Εξαιτίας του έντονου ανάγλυφου της Τενερίφης οι τιμές της φασματικής ανάκλασης για μια τάξη μπορεί να ποικίλλουν σημαντικά ανάλογα με την γωνία του εισερχόμενος φωτός. Ως εκ τούτου, χρησιμοποιήσαμε ακόμη μια ραδιομετρική διαδικασία διόρθωσης για να μειώσουμε την επίδραση της τοπογραφίας. Πριν ξεκινήσουμε την επιβλεπόμενη ταξινόμηση αρχικά εκτελέσαμε μια μη επιβλεπόμενη συσσώρευση για την κάθε τάξη των δεδομένων εκπαίδευσης για την ανίχνευση υποτάξεων οι οποίες θα έπρεπε να αντιμετωπιστούν ξεχωριστά. Η μέθοδος της μη επιβλεπόμενης ταξινόμησης που χρησιμοποιήσαμε για αυτό τον σκοπό είναι η μέση τεχνική μετατόπισης που αναπτύχθηκε από τους Comaniciu και Meer (2002). Το αποτέλεσμα της συσσώρευσης ορίζει ένα νέο αριθμό (μεγαλύτερο από m=10) τάξεων στα υπάρχοντα σημεία εκπαίδευσης, οι οποίες μετά χρησιμοποιούνται ως στοιχεία εισόδου στις μεθόδους επιβλεπόμενης ταξινόμησης. Τέλος, λαμβάνουμε μια κατάτμηση της εικόνας στις 10 τάξεις που καθορίστηκαν προηγουμένως, ξανασημειώνοντας κάθε pixel σε κείνη την τάξη από την οποία η ετικέτα υπό-τάξης της προήλθε. | ||
| Γραμμή 43: | Γραμμή 43: | ||
ML ταξινόμηση: | ML ταξινόμηση: | ||
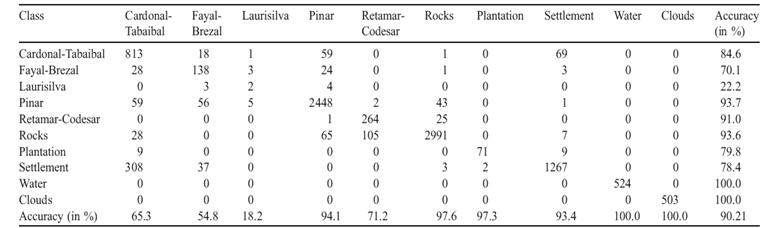
Διαφορετικές επιλογές για τις παραμέτρους δοκιμάστηκαν για την ταξινόμηση ML. Όσον αφορά τις μήτρες συνδιασποράς τα καλύτερα αποτελέσματα με συνολική cross-validation ακρίβεια του 90,21%±1,11%, λήφθηκαν με τη χρήση των πινάκων συνδιασποράς υπολογισμένων από τα δεδομένα εκπαίδευσης και κανονικοποιώντας τους με την προσθήκη μιας μικρής τιμής c=10-10 στη διαγώνιο. Χρησιμοποιώντας μεγαλύτερες τιμές για c πάντα έδινε καλύτερα αποτελέσματα για τις τάξεις που εκπροσωπούνται από λιγότερα δεδομένα εκπαίδευσης, αλλά υποβάθμιζε τα αποτελέσματα για τις άλλες τάξεις. Η χρήση γραμμικών ορίων απόφασης μέσω ενός κοινού πίνακα συνδιασποράς για όλες τις τάξεις απέδωσε μόνο μια συνολική ακρίβεια του 85,90%±1,35%. Η επιλογή των a priori πιθανοτήτων για τις διαφορετικές υποτάξεις είχαν σημαντική επίδραση στο αποτέλεσμα. Καθώς οι a priori πιθανότητες δόθηκαν μόνο για τις 10 προκαθορισμένες τάξεις (πίνακας 2) και όχι για τις υποτάξεις τους, που λήφθηκαν με μέση μετατόπιση, αυτές οι πιθανότητες έπρεπε να κατανέμονται καταλλήλως στις υποτάξεις. Στο πλαίσιο αυτό, τα καλύτερα στατιστικά αποτελέσματα προέκυψαν σταθμίζοντας την a priori πιθανότητα για την κάθε τάξη με τον σχετικό αριθμό δειγμάτων εκπαίδευσης από την κάθε αντίστοιχη υποτάξη. Για τα στοιχεία μελέτης της Τενερίφης που μας δόθηκαν, η τελευταία προσέγγιση πέτυχε μόνο μια συνολική crossvalidation ακρίβεια του 87,92%±1,23%, σε σύγκριση με το 90,21%±1,11% της πρώτης προσέγγισης. Από την άλλη πλευρά, με ομοιόμορφες a priori πιθανότητες για όλες τις υποτάξεις μια συνολική ακρίβεια του 88,86%±1,7% λήφθηκε.<br><br> | Διαφορετικές επιλογές για τις παραμέτρους δοκιμάστηκαν για την ταξινόμηση ML. Όσον αφορά τις μήτρες συνδιασποράς τα καλύτερα αποτελέσματα με συνολική cross-validation ακρίβεια του 90,21%±1,11%, λήφθηκαν με τη χρήση των πινάκων συνδιασποράς υπολογισμένων από τα δεδομένα εκπαίδευσης και κανονικοποιώντας τους με την προσθήκη μιας μικρής τιμής c=10-10 στη διαγώνιο. Χρησιμοποιώντας μεγαλύτερες τιμές για c πάντα έδινε καλύτερα αποτελέσματα για τις τάξεις που εκπροσωπούνται από λιγότερα δεδομένα εκπαίδευσης, αλλά υποβάθμιζε τα αποτελέσματα για τις άλλες τάξεις. Η χρήση γραμμικών ορίων απόφασης μέσω ενός κοινού πίνακα συνδιασποράς για όλες τις τάξεις απέδωσε μόνο μια συνολική ακρίβεια του 85,90%±1,35%. Η επιλογή των a priori πιθανοτήτων για τις διαφορετικές υποτάξεις είχαν σημαντική επίδραση στο αποτέλεσμα. Καθώς οι a priori πιθανότητες δόθηκαν μόνο για τις 10 προκαθορισμένες τάξεις (πίνακας 2) και όχι για τις υποτάξεις τους, που λήφθηκαν με μέση μετατόπιση, αυτές οι πιθανότητες έπρεπε να κατανέμονται καταλλήλως στις υποτάξεις. Στο πλαίσιο αυτό, τα καλύτερα στατιστικά αποτελέσματα προέκυψαν σταθμίζοντας την a priori πιθανότητα για την κάθε τάξη με τον σχετικό αριθμό δειγμάτων εκπαίδευσης από την κάθε αντίστοιχη υποτάξη. Για τα στοιχεία μελέτης της Τενερίφης που μας δόθηκαν, η τελευταία προσέγγιση πέτυχε μόνο μια συνολική crossvalidation ακρίβεια του 87,92%±1,23%, σε σύγκριση με το 90,21%±1,11% της πρώτης προσέγγισης. Από την άλλη πλευρά, με ομοιόμορφες a priori πιθανότητες για όλες τις υποτάξεις μια συνολική ακρίβεια του 88,86%±1,7% λήφθηκε.<br><br> | ||
| - | [[Εικόνα:Stlas_tener_5_05.jpg|center|image|]]<i>Πίνακας 3 : Crossvalidation αποτελέσματα για τον ταξινομητή ML. Κάθε γραμμή του πίνακα σύγχυσης δείχνει πως τα δεδομένα δοκιμών από μια τάξη είναι χαρακτηρισμένα, ενώ κάθε στήλη δείχνει ποία σημειακά δεδομένα είναι χαρακτηρισμένα έτσι ώστε να ανήκουν στην αντίστοιχη τάξη.[http://www.sciencedirect.com/science/article/pii/S0034425703001305]πηγή]]</i> | + | [[Εικόνα:Stlas_tener_5_05.jpg|center|image|]]<i>Πίνακας 3 : Crossvalidation αποτελέσματα για τον ταξινομητή ML. Κάθε γραμμή του πίνακα σύγχυσης δείχνει πως τα δεδομένα δοκιμών από μια τάξη είναι χαρακτηρισμένα, ενώ κάθε στήλη δείχνει ποία σημειακά δεδομένα είναι χαρακτηρισμένα έτσι ώστε να ανήκουν στην αντίστοιχη τάξη.[http://www.sciencedirect.com/science/article/pii/S0034425703001305]πηγή]]</i><br> |
[[Εικόνα:Stlas_tener_6_05.gif|right|thumb||Εικόνα 3 : Το αποτέλεσμα του ταξινομητή ML, χρησιμοποιώντας όλα τα διαθέσιμα δείγματα εκπαίδευσης (βλ. εικόνα 2 για τους κωδικούς των χρωμάτων). Τα μαύρα pixels υποδεικνύουν τα σημειακά δεδομένα που έχουν ανατεθεί στην έξω-τάξη.[http://www.sciencedirect.com/science/article/pii/S0034425703001305]πηγή]] | [[Εικόνα:Stlas_tener_6_05.gif|right|thumb||Εικόνα 3 : Το αποτέλεσμα του ταξινομητή ML, χρησιμοποιώντας όλα τα διαθέσιμα δείγματα εκπαίδευσης (βλ. εικόνα 2 για τους κωδικούς των χρωμάτων). Τα μαύρα pixels υποδεικνύουν τα σημειακά δεδομένα που έχουν ανατεθεί στην έξω-τάξη.[http://www.sciencedirect.com/science/article/pii/S0034425703001305]πηγή]] | ||
ICM ταξινόμηση: | ICM ταξινόμηση: | ||
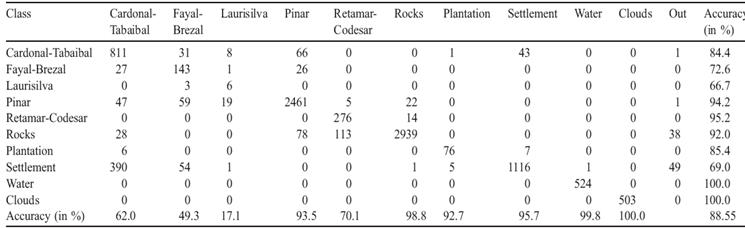
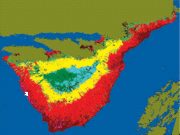
Ο αλγόριθμος ICM θα πρέπει να βελτιώσει το αποτέλεσμα της ταξινόμησης του ταξινομητή ML με τη χρήση χωρικού πλαισίου, Ξεκινήσαμε τον ICM με την ταξινόμηση που παρατίθεται στην εικόνα 3 και τον τρέξαμε για 10 επαναλήψεις. Το ενδιαφέρον αποτέλεσμα είναι ότι η crossvalidation ακρίβεια βελτιώθηκε μετά την πρώτη επανάληψη. Μετά τα μέσα διανύσματα και τους πίνακες συνδιασποράς που ξανά υπολογίστηκαν από την προηγούμενη ταξινόμηση, ο αριθμός των σωστά ταξινομημένων pixels μειώνονταν με κάθε διαδοχική επανάληψη, με την κάθε τάξη εδαφοκάλυψης να επηρεάζεται εξίσου. Το πρόβλημα της μείωσης της ακρίβειας μπορεί βεβαίως να παρακαμφθεί με την αποφυγή της επανεκτίμησης των παραμέτρων και με τη χρήση των αρχικών μέσων διανυσμάτων και πινάκων συνδιασποράς που υπολογίζονται από τα δεδομένα εκπαίδευσης σε όλο τον αλγόριθμο. Σε αυτή την περίπτωση, πράγματι, με κάθε επανάληψη μια υψηλότερη ακρίβεια λήφθηκε και ο αλγόριθμος σύγκλινε μετά από μερικά βήματα, με συνολική ακρίβεια περίπου 91%. Παρόλου που ο ICM χρησιμοποιείται στις περισσότερες εφαρμογές, απέχουμε από αυτή τη διαδικασία, καθώς συνήθως χρειάζεται ακριβείς αρχικές εκτιμήσεις των παραμέτρων, για τις οποίες δεν μπορούμε να εγγυηθούμε στην περίπτωση που εξετάζεται στο παρόν έγγραφο. Επιπλέον, τα αποτελέσματα που επιτεύχθηκαν με αυτόν τον τρόπο δεν ήταν οπτικά πειστικά, καθώς εξακολουθούσαν να περιέχουν πολύ θόρυβο. Επομένως, ως συμβιβαστική λύση θα αναλύσουμε τα αποτελέσματα του αλγορίθμου ICM μετά από 5 επαναλήψεις, με αυτών τον τρόπο αποφεύγεται η υπερβολική φθορά, αλλά εξακολουθείται να επιτρέπεται ένα σημαντικό ποσό εξομάλυνσης. Η αντίστοιχη ταξινόμηση παρουσιάζεται στη εικόνα 4, και πάλι τα μαύρα pixels δηλώνουν αυτά τα σημειακά στοιχεία που ανατέθηκαν στην έξω-τάξη. Σε αυτή την περίπτωση, μια συνολική crossvalidation ακρίβεια του 88,55%±1,35% επιτεύχθηκε. Συγκριτικά, η αντίστοιχη ακρίβεια της αρχικής λύσης που λήφθηκε από την ML ήταν 89,18%±1,11%. Παρόλα αυτά, το αποτέλεσμα της ταξινόμησης ICM είναι οπτικά πιο ικανοποιητικό από αυτό της ML, καθώς είναι λιγότερο θορυβώδες. Η σύγκριση του πλήρους πίνακα σύγχυσης για την ICM δίνεται στον πίνακα 4.<br><br> | Ο αλγόριθμος ICM θα πρέπει να βελτιώσει το αποτέλεσμα της ταξινόμησης του ταξινομητή ML με τη χρήση χωρικού πλαισίου, Ξεκινήσαμε τον ICM με την ταξινόμηση που παρατίθεται στην εικόνα 3 και τον τρέξαμε για 10 επαναλήψεις. Το ενδιαφέρον αποτέλεσμα είναι ότι η crossvalidation ακρίβεια βελτιώθηκε μετά την πρώτη επανάληψη. Μετά τα μέσα διανύσματα και τους πίνακες συνδιασποράς που ξανά υπολογίστηκαν από την προηγούμενη ταξινόμηση, ο αριθμός των σωστά ταξινομημένων pixels μειώνονταν με κάθε διαδοχική επανάληψη, με την κάθε τάξη εδαφοκάλυψης να επηρεάζεται εξίσου. Το πρόβλημα της μείωσης της ακρίβειας μπορεί βεβαίως να παρακαμφθεί με την αποφυγή της επανεκτίμησης των παραμέτρων και με τη χρήση των αρχικών μέσων διανυσμάτων και πινάκων συνδιασποράς που υπολογίζονται από τα δεδομένα εκπαίδευσης σε όλο τον αλγόριθμο. Σε αυτή την περίπτωση, πράγματι, με κάθε επανάληψη μια υψηλότερη ακρίβεια λήφθηκε και ο αλγόριθμος σύγκλινε μετά από μερικά βήματα, με συνολική ακρίβεια περίπου 91%. Παρόλου που ο ICM χρησιμοποιείται στις περισσότερες εφαρμογές, απέχουμε από αυτή τη διαδικασία, καθώς συνήθως χρειάζεται ακριβείς αρχικές εκτιμήσεις των παραμέτρων, για τις οποίες δεν μπορούμε να εγγυηθούμε στην περίπτωση που εξετάζεται στο παρόν έγγραφο. Επιπλέον, τα αποτελέσματα που επιτεύχθηκαν με αυτόν τον τρόπο δεν ήταν οπτικά πειστικά, καθώς εξακολουθούσαν να περιέχουν πολύ θόρυβο. Επομένως, ως συμβιβαστική λύση θα αναλύσουμε τα αποτελέσματα του αλγορίθμου ICM μετά από 5 επαναλήψεις, με αυτών τον τρόπο αποφεύγεται η υπερβολική φθορά, αλλά εξακολουθείται να επιτρέπεται ένα σημαντικό ποσό εξομάλυνσης. Η αντίστοιχη ταξινόμηση παρουσιάζεται στη εικόνα 4, και πάλι τα μαύρα pixels δηλώνουν αυτά τα σημειακά στοιχεία που ανατέθηκαν στην έξω-τάξη. Σε αυτή την περίπτωση, μια συνολική crossvalidation ακρίβεια του 88,55%±1,35% επιτεύχθηκε. Συγκριτικά, η αντίστοιχη ακρίβεια της αρχικής λύσης που λήφθηκε από την ML ήταν 89,18%±1,11%. Παρόλα αυτά, το αποτέλεσμα της ταξινόμησης ICM είναι οπτικά πιο ικανοποιητικό από αυτό της ML, καθώς είναι λιγότερο θορυβώδες. Η σύγκριση του πλήρους πίνακα σύγχυσης για την ICM δίνεται στον πίνακα 4.<br><br> | ||
| - | [[Εικόνα:Stlas_tener_7_05.jpg|center|image|]]<i>Πίνακας 4 : Crossvalidation αποτελέσματα για τον ταξινομητή ICM. Σε αντίθεση με την ML, ο πίνακας σύγχυσης περιέχει μια πρόσθετη στήλη για να υποδείξει τα pixels που ανατέθηκαν στην έξω-τάξη.[http://www.sciencedirect.com/science/article/pii/S0034425703001305]πηγή]]</i> | + | [[Εικόνα:Stlas_tener_7_05.jpg|center|image|]]<i>Πίνακας 4 : Crossvalidation αποτελέσματα για τον ταξινομητή ICM. Σε αντίθεση με την ML, ο πίνακας σύγχυσης περιέχει μια πρόσθετη στήλη για να υποδείξει τα pixels που ανατέθηκαν στην έξω-τάξη.[http://www.sciencedirect.com/science/article/pii/S0034425703001305]πηγή]]</i><br> |
[[Εικόνα:Stlas_tener_8_05.gif|right|thumb||Εικόνα 4 : Το αποτελέσματα του ταξινομητή ICM μετά από 5 επαναλήψεις, χρησιμοποιώντας το αποτέλεσμα του ταξινομητή ML ως αρχική εκτίμηση (βλ. εικόνα 2 για τους κωδικούς των χρωμάτων). Τα μαύρα pixels υποδεικνύουν τα σημειακά δεδομένα που έχουν ανατεθεί στην έξω-τάξη.[http://www.sciencedirect.com/science/article/pii/S0034425703001305]πηγή]] | [[Εικόνα:Stlas_tener_8_05.gif|right|thumb||Εικόνα 4 : Το αποτελέσματα του ταξινομητή ICM μετά από 5 επαναλήψεις, χρησιμοποιώντας το αποτέλεσμα του ταξινομητή ML ως αρχική εκτίμηση (βλ. εικόνα 2 για τους κωδικούς των χρωμάτων). Τα μαύρα pixels υποδεικνύουν τα σημειακά δεδομένα που έχουν ανατεθεί στην έξω-τάξη.[http://www.sciencedirect.com/science/article/pii/S0034425703001305]πηγή]] | ||
SVM ταξινόμηση: | SVM ταξινόμηση: | ||
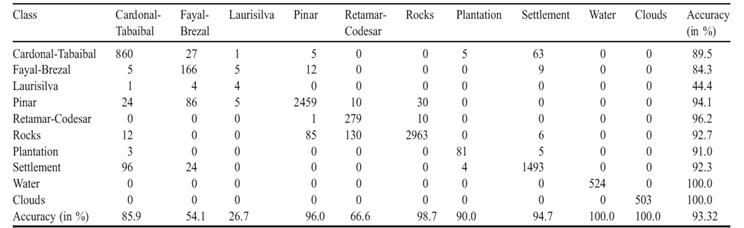
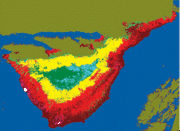
Η προ επεξεργασία των δεδομένων με μέσημετατόπιση δεν βοήθησε την SVM να βρει καλύτερες ταξινομήσεις. Αυτό δεν προκαλεί έκπληξη καθώς, σε αντίθεση με την ML και την ICM, η SVM δεν αναλαμβάνει τις τάξεις που έχουν κατανεμηθεί μονοτροπικά. Ο πίνακας 5 δίνει τον πίνακα σύγχυσης για την SVM που εκπαιδεύεται σε ένα υποσύνολο των crossvalidation στοιχείων εκπαίδευσης και εξετάζεται στα ίδια δεδομένα όπως οι ταξινομητές ML και ICM. Σημειώνεται, ότι στις τάξεις όπου μόνο λίγα δεδομένα εκπαίδευσης είναι διαθέσιμα, η ακρίβεια της ταξινόμησης είναι σοβαρά μειωμένη. Η συνολική ακρίβεια του 93,32%±0.61% είναι απρόσμενα καλή και μάλλον αισιόδοξα προκατειλημμένη: έχουμε πολύ λίγα επίγεια δεδομένα στο χέρι μας και η διακύμανση της τάξης που πάρθηκε από αυτό το δείγμα μπορεί να είναι μικρότερη από την πραγματική διακύμανση εντός των τάξεων. Η εικόνα 5 απεικονίζει μια ταξινόμηση ολόκληρου του νησιού βασισμένη σε 10.000 τυχαία επιλεγμένα διανύσματα. Συγκρίνοντας, αυτό το αποτέλεσμα με την ταξινόμηση ML αμέσως αντιλαμβανόμαστε ότι ο ταξινομητής SVM απλώνει ένα μεγάλο ποσό της τάξης οικισμός κατά μήκος της νοτιοανατολικής ακτής: σε αυτή την περιοχή , τα επίγεια δεδομένα είναι σπάνια έτσι ο SVM αποφασίζει για τον οικισμό. Επίσης, ο ML λανθασμένα ανιχνεύει οικισμό κατά μήκος της νοτιοανατολικής ακτής, αλλά καθώς ο ML αξιοποιεί a priori τις πληροφορίες για τις πιθανότητες τάξης, κατατάσσει το μεγαλύτερο μέρος της αταξινόμητης περιοχής στην τάξη Cardonal&Tabaibal η οποία είναι ίσως η σωστή ταξινόμηση.<br><br> | Η προ επεξεργασία των δεδομένων με μέσημετατόπιση δεν βοήθησε την SVM να βρει καλύτερες ταξινομήσεις. Αυτό δεν προκαλεί έκπληξη καθώς, σε αντίθεση με την ML και την ICM, η SVM δεν αναλαμβάνει τις τάξεις που έχουν κατανεμηθεί μονοτροπικά. Ο πίνακας 5 δίνει τον πίνακα σύγχυσης για την SVM που εκπαιδεύεται σε ένα υποσύνολο των crossvalidation στοιχείων εκπαίδευσης και εξετάζεται στα ίδια δεδομένα όπως οι ταξινομητές ML και ICM. Σημειώνεται, ότι στις τάξεις όπου μόνο λίγα δεδομένα εκπαίδευσης είναι διαθέσιμα, η ακρίβεια της ταξινόμησης είναι σοβαρά μειωμένη. Η συνολική ακρίβεια του 93,32%±0.61% είναι απρόσμενα καλή και μάλλον αισιόδοξα προκατειλημμένη: έχουμε πολύ λίγα επίγεια δεδομένα στο χέρι μας και η διακύμανση της τάξης που πάρθηκε από αυτό το δείγμα μπορεί να είναι μικρότερη από την πραγματική διακύμανση εντός των τάξεων. Η εικόνα 5 απεικονίζει μια ταξινόμηση ολόκληρου του νησιού βασισμένη σε 10.000 τυχαία επιλεγμένα διανύσματα. Συγκρίνοντας, αυτό το αποτέλεσμα με την ταξινόμηση ML αμέσως αντιλαμβανόμαστε ότι ο ταξινομητής SVM απλώνει ένα μεγάλο ποσό της τάξης οικισμός κατά μήκος της νοτιοανατολικής ακτής: σε αυτή την περιοχή , τα επίγεια δεδομένα είναι σπάνια έτσι ο SVM αποφασίζει για τον οικισμό. Επίσης, ο ML λανθασμένα ανιχνεύει οικισμό κατά μήκος της νοτιοανατολικής ακτής, αλλά καθώς ο ML αξιοποιεί a priori τις πληροφορίες για τις πιθανότητες τάξης, κατατάσσει το μεγαλύτερο μέρος της αταξινόμητης περιοχής στην τάξη Cardonal&Tabaibal η οποία είναι ίσως η σωστή ταξινόμηση.<br><br> | ||
| - | [[Εικόνα:Stlas_tener_9_05.jpg|center|image|]]<i>Πίνακας 5 : Crossvalidation αποτελέσματα για τον ταξινομητή SVM. Ο SVM έτρεξε σε ένα τυχαία επιλεγμένο υποσύνολο των Crossvalidation δεδομένων εκπαίδευσης. Τα δεδομένα δοκιμών είναι τα ίδια με αυτά των ταξινομητών ML και ICM.[http://www.sciencedirect.com/science/article/pii/S0034425703001305]πηγή]]</i> | + | [[Εικόνα:Stlas_tener_9_05.jpg|center|image|]]<i>Πίνακας 5 : Crossvalidation αποτελέσματα για τον ταξινομητή SVM. Ο SVM έτρεξε σε ένα τυχαία επιλεγμένο υποσύνολο των Crossvalidation δεδομένων εκπαίδευσης. Τα δεδομένα δοκιμών είναι τα ίδια με αυτά των ταξινομητών ML και ICM.[http://www.sciencedirect.com/science/article/pii/S0034425703001305]πηγή]]</i><br> |
[[Εικόνα:Stlas_tener_10_05.gif|right|thumb||Εικόνα 5 : Το αποτέλεσμα του ταξινομητή SVM που έτρεξε σε ένα υποσύνολο 10.000 τυχαία επιλεγμένων διανυσμάτων εκπαίδευσης (βλ. εικόνα 2 για τους κωδικούς των χρωμάτων).[http://www.sciencedirect.com/science/article/pii/S0034425703001305]πηγή]] | [[Εικόνα:Stlas_tener_10_05.gif|right|thumb||Εικόνα 5 : Το αποτέλεσμα του ταξινομητή SVM που έτρεξε σε ένα υποσύνολο 10.000 τυχαία επιλεγμένων διανυσμάτων εκπαίδευσης (βλ. εικόνα 2 για τους κωδικούς των χρωμάτων).[http://www.sciencedirect.com/science/article/pii/S0034425703001305]πηγή]] | ||
Αναθεώρηση της 20:14, 30 Ιανουαρίου 2012
Αυτόματη ανάλυση της κάλυψης εδάφους για την Τενερίφη με Επιβλεπόμενη Ταξινόμηση χρησιμοποιώντας τηλεπισκοπικά δεδομένα
Automatic land cover analysis for Tenerife by supervised classification using remotely sensed data
Jens Keuchel, Simone Naumann, Matthias Heiler, Alexander Siegmund , Remote Sensing of Environment, Volume 86, Issue 4, 30 August 2003, Pages 530-541
[6]
Περίληψη
Η αυτόματη ταξινόμηση της κάλυψης του εδάφους από δορυφορικές εικόνες είναι ένα σημαντικό θέμα σε πολλές εφαρμογές τηλεπισκόπησης. Σε αυτή την εργασία, εξετάζουμε τρεις διαφορετικές στατιστικές προσεγγίσεις για την αντιμετώπιση του προβλήματος: δυο από αυτές, δηλαδή η γνωστή ταξινόμηση Μεγίστης Πιθανοφάνειας (ML) και η Διανυσματική Μηχανή Υποστήριξης (SVM) είναι μη συναφείς μέθοδοι. Η τρίτη, Επαναλαμβανόμενα Υποθετικά Μοντέλα (ICM), εκμεταλλεύεται το χωρικό πλαίσιο χρησιμοποιώντας ένα τυχαίο πεδίο Markov. Εφαρμόσαμε αυτές τις μεθόδους σε δεδομένα Landsat 5 TM από την Τενερίφη, το μεγαλύτερο των Καναρίων Νησιών. Δείχνουμε ότι μετά την εφαρμογή μιας μη επιβλεπόμενης μεθόδου ομαδοποίησης για τον καθορισμό υπό κατηγοριών, όλοι οι αλγόριθμοι ταξινόμησης έδωσαν ικανοποιητικά αποτελέσματα (με συνολική στατιστική ακρίβεια της τάξης του 90%) αν οι παράμετροι του μοντέλου συλλέγονται κατάλληλα. Παρά το γεγονός ότι θεωρητικά είναι ανώτερες της ML, και οι δύο SVM και ICM πρέπει να χρησιμοποιηθούν προσεκτικά: η μέθοδος ICM είναι ικανή να βελτιώσει την μέθοδο ML, αλλά όταν εφαρμόζεται για πάρα πολλές επαναλήψεις, χωρικά οι μικρές περιοχές εξομαλύνονται, οδηγώντας σε στατιστικά ελαφρώς χειρότερα αποτελέσματα ταξινόμησης. Η μέθοδος SVM παράγει καλύτερα στατιστικά αποτελέσματα από την ML, αλλά όταν ερευνήθηκε οπτικά, το αποτέλεσμα της ταξινόμησης δεν ήταν πλήρως ικανοποιητικό. Αυτό οφείλεται στο γεγονός ότι καμία a priori πληροφορία για την συχνότητα εμφάνισης μιας τάξης δεν χρησιμοποιήθηκε σε αυτό το πλαίσιο, το οποίο βοηθά τη μέθοδο ML να περιορίσει τις μη πιθανές τάξεις.
Εισαγωγή
Η αυτόματη ανάλυση τηλεπισκοπικών δεδομένων γίνεται όλο και σημαντικότερη κατά τις τελευταίες δεκαετίες. Ιδιαίτερα η κατάτμηση των δορυφορικών εικόνων σε περιοχές με διαφορετική κάλυψη εδάφους είναι μείζονος ενδιαφέροντος: λαμβάνοντας υπόψη τα δεδομένα από διάφορα φασματικά κανάλια, θέλει να καθορίσει για κάθε pixel της εικόνας τον τύπο εδαφοκάλυψης που είναι παρόν στην αντίστοιχη περιοχή της επιφάνειας. Το νησί της Τενερίφης είναι ιδιαίτερα ενδιαφέρουσα περιοχή μελέτης για αυτό το σκοπό καθώς, λόγω της μεγάλης κάθετης έκτασης του και της θέσης του στον Ατλαντικό, προσφέρει ένα ευρύ φάσμα διαφορετικών τάξεων βλάστησης. Ωστόσο, η μεγάλη έκταση και το έντονο ανάγλυφο του νησιού αύξησε το πρόβλημα της αραιής συλλογής των στοιχείων εκπαίδευσης. Επιπλέον οι φασματικές ανακλάσεις που καταγράφθηκαν από το δορυφορικό δέκτη μπορεί να ποικίλουν μέσα σε μια τάξη εδαφοκάλυψης ανάλογα με την κλίση και την πλευρά. Επομένως, η κατάλληλη προ επεξεργασία των δεδομένων των 7 καναλιών του Landsat 5 ΤΜ με τη βοήθεια ενός ψηφιακού μοντέλου υψομέτρων είναι ουσιαστική για την επιτυχία της επακόλουθης διαδικασίας ταξινόμησης. Οι φασματικοί ταξινομητές συνήθως διακρίνονται σε παραμετρικούς και μη παραμετρικούς. Μελετάμε επιβλεπόμενους ταξινομητές και από τις δυο κατηγορίες: από την μια πλευρά ο γνωστός αλγόριθμος της Μεγίστης Πιθανοφάνειας ML είναι μια παραμετρική μέθοδος, η οποία προϋποθέτει μια ειδική κατανομή πιθανοτήτων (συνήθως μια Γκαουσιανή κατανομή) των δοθέντων στοιχείων a priori και καθορίζει τις κατάλληλες παραμέτρους (μέσο διάνυσμα και πίνακα συνδιασποράς) από τα δεδομένα εκπαίδευσης. Κάθε σημειακό δεδομένο τότε, κατατάσσεται στην τάξη για την οποία η τιμή του είναι πιο πιθανή, δηλαδή στη τάξη με την μεγαλύτερη a posteriori πιθανότητα. Από την άλλη πλευρά, οι Διανυσματικές Μηχανές Υποστήριξης (SVMs) ανήκουν στην κατηγορία των μη παραμετρικών μεθόδων, οι οποίες δεν επιχειρούν να διαμορφώσουν την κατανομή των δεδομένων, αλλά προσπαθούν να διαχωρίσουν τις διαφορετικές τάξεις με την απευθείας αναζήτηση επαρκών ορίων μεταξύ τους. Το πλεονέκτημα αυτής της προσέγγισης είναι ότι γενικεύει καλά, ακόμα και αν λειτουργεί με μικρό αριθμό δειγμάτων. Και οι δύο προσεγγίσεις πάσχουν από το μειονέκτημα ότι συνήθως παράγουν θορυβώδεις κατατμήσεις. Αυτό το φαινόμενο προκαλείται κυρίως από τον σημαντικό θόρυβο στα δεδομένα εισόδου εξαιτίας της ανακλαστηκότητας των γειτονικών pixel. Μια ελκυστική στρατηγική για την αντιμετώπιση αυτών των προβλημάτων είναι να αξιοποιηθεί το χωρικό πλαίσιο, όπου εκτός από τις φασματικές τιμές για το κάθε pixel, αξιολογούνται επίσης και οι πληροφορίες από τα γειτονικά pixels. Από αυτή την άποψη, δοκιμάσαμε τον αλγόριθμο ICM στα δεδομένα εικόνας μας. Βασικά, αυτή η παραμετρική μέθοδος διαμορφώνει a priori την κατανομή της εικόνας ως ένα τοπικά εξαρτώμενο τυχαίο πεδίο Markov, για το οποίο η μέγιστη a posteriori εκτίμηση προσεγγίζεται επαναληπτικά. Μετά την απόκτηση μιας πρώτης εκτίμησης χρησιμοποιώντας κάποια μη συναφή μέθοδο όπως την ML ή την SVΜ, σε κάθε βήμα επανάληψης κάθε pixel κατατάσσεται στην τάξη που είναι πιθανότερη δεδομένου των φασματικών του τιμών και τις παρούσες ετικέτες των γειτόνων του. Αυτό οδηγεί σε μια τελική κατάτμηση η οποία είναι ομαλότερη και λιγότερο ευαίσθητη στο θόρυβο από τα αποτελέσματα των μη συναφών μεθόδων. Σε αυτή την εργασία θα συγκρίνουμε αυτούς τους τρεις αλγορίθμους επιβλεπόμενης ταξινόμησης και θα συζητήσουμε τα πλεονεκτήματα τους και τα όριά τους, στο πλαίσιο της αυτόματης ανάλυσης εικόνων Landsat ΤΜ ενός τοπίου με έντονα ανώμαλο έδαφος για το οποίο τα δεδομένα εκπαίδευσης παρέχονται μόνο αραιά.
Περιοχή Μελέτης - Μέθοδοι
Η περιοχή μελέτης για την αυτόματη ανάλυση της κάλυψης εδάφους είναι η Τενερίφη, με περίπου 2050 km2 το μεγαλύτερο από τα Κανάρια Νησιά. Λόγω της κάθετης και οριζόντιας έκτασής του καθώς και της θέσης του στη μέση του Ατλαντικού, το κλίμα της Τενερίφης και η βλάστηση ποικίλλουν έντονα. Λόγω της ετερογενούς φυσικής και καλλιεργήσιμης έκτασης, πολλές διαφορετικές τάξεις εδαφοκάλυψης έπρεπε να ληφθούν υπόψη. Από τη μια πλευρά οι τάξεις που προκύπτουν από τις μη επιβλεπόμενες ταξινομήσεις (ανάλυση συσσωρεύσεων), και από την άλλη πλευρά αυτές που προκύπτουν από τους επίγειους ελέγχους. Εξαιτίας της χονδροειδούς ανάλυσης των δορυφορικών εικόνων και του υψηλού αριθμού διαφορετικών τάξεων κάλυψης εδάφους, ήταν αναπόφευκτο να μειωθεί αυτός ο αριθμός με την τοποθέτηση των παρόμοιων τάξεων μαζί. Τελικά, αφού έγιναν όλες οι τεχνικές και γεωγραφικές εκτιμήσεις για την επιλογή των τάξεων, αποφασίσαμε να χρησιμοποιήσουμε m= 10 τάξεις στην αυτόματη ανάλυση της κάλυψης εδάφους για την Τενερίφη (πίνακας 1).
Οι δορυφορικές εικόνες που χρησιμοποιήθηκαν σε αυτή τη μελέτη είχαν ληφθεί στις 7 Αυγούστου 1988 από τον Landsat 5 ΤΜ. Επίσης ήταν χρήσιμο να χρησιμοποιήσουμε ένα Ψηφιακό Μοντέλο Υψομέτρων DEM για την κωδικοποίηση των υψομετρικών δεδομένων, έτσι ώστε να μπορεί να ενσωματωθεί στη διαδικασία της ταξινόμησης αργότερα. Στην εικόνα Landsat TM της Τενερίφης που μας δόθηκε, κάποιο μέρος του νησιού δυστυχώς καλύπτεται από σύννεφο. Για να μην έχουμε αρνητική επίδραση κατά τη ταξινόμηση, αυτά τα σύννεφα απομακρύνθηκαν εκ των προτέρων από τα κανάλια εισόδου. Εξαιτίας του έντονου ανάγλυφου της Τενερίφης οι τιμές της φασματικής ανάκλασης για μια τάξη μπορεί να ποικίλλουν σημαντικά ανάλογα με την γωνία του εισερχόμενος φωτός. Ως εκ τούτου, χρησιμοποιήσαμε ακόμη μια ραδιομετρική διαδικασία διόρθωσης για να μειώσουμε την επίδραση της τοπογραφίας. Πριν ξεκινήσουμε την επιβλεπόμενη ταξινόμηση αρχικά εκτελέσαμε μια μη επιβλεπόμενη συσσώρευση για την κάθε τάξη των δεδομένων εκπαίδευσης για την ανίχνευση υποτάξεων οι οποίες θα έπρεπε να αντιμετωπιστούν ξεχωριστά. Η μέθοδος της μη επιβλεπόμενης ταξινόμησης που χρησιμοποιήσαμε για αυτό τον σκοπό είναι η μέση τεχνική μετατόπισης που αναπτύχθηκε από τους Comaniciu και Meer (2002). Το αποτέλεσμα της συσσώρευσης ορίζει ένα νέο αριθμό (μεγαλύτερο από m=10) τάξεων στα υπάρχοντα σημεία εκπαίδευσης, οι οποίες μετά χρησιμοποιούνται ως στοιχεία εισόδου στις μεθόδους επιβλεπόμενης ταξινόμησης. Τέλος, λαμβάνουμε μια κατάτμηση της εικόνας στις 10 τάξεις που καθορίστηκαν προηγουμένως, ξανασημειώνοντας κάθε pixel σε κείνη την τάξη από την οποία η ετικέτα υπό-τάξης της προήλθε.

Ο αλγόριθμος της Μεγίστης Πιθανοφάνειας ML ανήκει στη κατηγορία των παραμετρικών μεθόδων ταξινόμησης. Αυτό σημαίνει ότι τα στοιχεία υποτίθεται ότι διανεμήθηκαν σύμφωνα με ένα προηγουμένως καθορισμένο μοντέλο πιθανότητας, για το οποίο οι παράμετροι καθορίζονται από ένα δοσμένο σύνολο εκπαίδευσης. Κάθε σημειακό δεδομένο ταξινομείται έπειτα ανεξάρτητα, επονομάζοντας το ώστε να ανήκει στη τάξη η οποία είναι η πιο πιθανή, δηλαδή που έχει τη μεγαλύτερη a posteriori πιθανότητα. Για τον υπολογισμό αυτών των πιθανοτήτων χρησιμοποιείται ο κανόνας Bayes. Ακόμη, για να υπολογιστεί η πιθανότητα, μια πολυμεταβλητή Γκαουσιανή κατανομή θεωρείται για κάθε τάξη. Μετά την προεπεξεργασία των δεδομένων εκπαίδευσης με μια μη επιβλεπόμενη μέθοδο ταξινόμησης, ο αριθμός των δειγμάτων εκπαίδευσης μπορεί να γίνει αρκετά μικρός για μερικές τάξεις. Αυτό μπορεί να οδηγήσει σε αναξιόπιστες εκτιμήσεις των αντίστοιχων μητρών συνδιασποράς. Καθώς τα σημεία εκπαίδευσης συλλέχθηκαν συνήθως από αρκετά συνεκτικές περιοχές (τάξη νερού), η διασπορά που λαμβάνεται από τα στοιχεία εκπαίδευσης ενδέχεται να είναι χαμηλότερη από τη πραγματική διασπορά της κατανομής της αντίστοιχης τάξης. Ένας τρόπος για να χειριστεί τις ακραίες τιμές στα δεδομένα που δεν ταιριάζουν σε καμία από τις προκαθορισμένες τάξεις, είναι να καθορίσει μια πρόσθετη έξω-τάξη. Στην εφαρμογή μας, ανακαλύψαμε κάποια μειονεκτήματα του ταξινομητή ML. Η ταξινόμηση είναι αποκλειστικά βασισμένη στις φασματικές πληροφορίες για κάθε pixel χωρίς να χρησιμοποιεί τις πληροφορίες από τα γειτονικά pixels, το οποίο συνήθως οδηγεί σε ένα θορυβώδες αποτέλεσμα ταξινόμησης. Επιπλέον, η σταθερή μορφή των ορίων απόφασης απαγορεύει μια λεπτομερή ρύθμιση στα δεδομένα εκπαίδευσης.
Ο αλγόριθμος ICM χρησιμοποιεί την ίδια μέθοδο ταξινόμησης όπως ο ML: βασισμένη στον κανόνα Bayes, σε κάθε σημειακό δεδομένο ανατίθεται η ετικέτα που είναι η πιο πιθανή. Η διαφορά είναι το υποκείμενο μοντέλο πιθανότητας: εκτιμώντας ότι ο ταξινομητής ML χρησιμοποιεί μόνο τη φασματική πληροφορία για κάθε σημειακό στοιχείο για να υπολογίσει τις a posteriori πιθανότητες, ο αλγόριθμος ICM ενσωματώνει επίσης το χωρικό πλαίσιο. Για το σκοπό αυτό, θεωρείται ότι η πραγματική εικόνα είναι η υλοποίηση ενός τοπικά εξαρτώμενου τυχαίου πεδίου Markov, έτσι ώστε η πιθανότητα μιας ετικέτας για ένα συγκεκριμένο σημειακό στοιχείο εξαρτάται επίσης από την επονομασία των γειτόνων του. Η a priori πιθανότητα μιας ετικέτας αντικαταστάθηκε από την υπό όρους πιθανότητα η οποία εξαρτάται από τις ετικέτες γύρω από το σημειακό δεδομένο.
Οι SVM είναι διακριτικοί δυαδικοί ταξινομητές, δηλαδή σε αντίθεση με τους αλγόριθμους ταξινόμησης που περιγράφτηκαν παραπάνω, οι SVM δεν επιχειρούν να διαμορφώσουν την κατανομή της πιθανότητας των διανυσμάτων εκπαίδευσης. Αντ’ αυτού, η συνάρτηση απόφασης λαμβάνεται από τα σημειακά δεδομένα εκπαίδευσης ως η λύση στο πρόβλημα τακτοποίησης σε ένα κατάλληλο διάστημα Hilbert καθορισμένο από έναν συμμετρικό, θετικά ορισμένο πυρήνα λειτουργίας. Οι ετικέτες των τάξεων των σημείων εκπαίδευσης κωδικοποιούνται ως αριθμοί. Αφού η δυαδική συνάρτηση απόφασης έχει καθοριστεί, κάθε σημειακό στοιχείο μπορεί να επισημανθεί σύμφωνα με το αν το αποτέλεσμα της συνάρτησης είναι θετικό ή αρνητικό. Η επιλογή του πυρήνα λειτουργίας είναι σημαντική για την καλή απόδοση της ταξινόμησης. Στα πειράματα μας χρησιμοποιήσαμε τον Γκαουσιανό ακτινικής βάσης πυρήνα λειτουργίας. Μια δημοφιλής προσέγγιση είναι να χωριστεί ένα πολυταξικό πρόβλημα σε πολλαπλά δυαδικά προβλήματα, τα οποία μπορούν να αντιμετωπιστούν από τους πρότυπους SVΜs. Η μέθοδος αυτή είναι αποτελεσματική από άποψη ταχύτητας και ακρίβειας της ταξινόμησης.
Αποτελέσματα
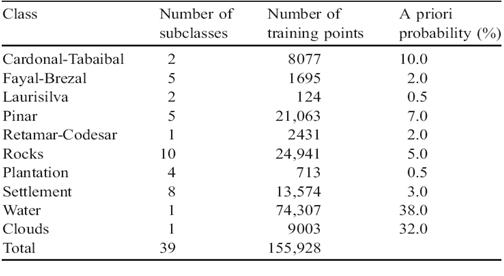
Σε αυτή την ενότητα παρουσιάζουμε τα αποτελέσματα που προέκυψαν από τις διαφορετικές μεθόδους ταξινόμησης. Εκτενής προμελέτη αποκάλυψε ότι τα καλύτερα αποτελέσματα επιτεύχθηκαν όταν όλα και τα 7 φασματικά κανάλια από τον Landsat 5 TM χρησιμοποιήθηκαν συγχρόνως ως δεδομένα εισόδου. Η εικόνα 2, δείχνει μια προβολή των σημειακών δεδομένων μελέτης πάνω στο δισδιάστατο διάστημα που εκτείνεται από τα κανάλια 4 και 7. Αν και αυτό είναι ο συνδυασμός δυο καναλιών, όπου τα σημειακά δεδομένα οπτικά εξαπλώνονται πιο πολύ, οι τάξεις είναι ιδιαίτερα επικαλυπτόμενες, με μόνη εξαίρεση τις τάξεις που αντιπροσωπεύουν το νερό και τα σύννεφα. Οι συσσωρεύσεις που περιέχουν λιγότερα από 5 σημειακά δεδομένα θεωρήθηκαν ως ακραίες τιμές και απομακρύνθηκαν από τα δεδομένα μελέτης. Αυτό είχε ως αποτέλεσμα m=39 υποτάξεις με συνολικά n=155.928 δείγματα εκπαίδευσης όπως φαίνεται στον πίνακα 2, με 11 υποτάξεις που περιέχουν λιγότερα από 20 δείγματα.

Πίνακας 2 : Ο αριθμός των υποτάξεων που λαμβάνονται με μέση μετατόπιση, ο αντίστοιχος συνολικός αριθμός των σημείων εκπαίδευσης και οι a priori πιθανότητες για κάθε προκαθορισμένη τάξη.[8]πηγή]]
ML ταξινόμηση:
Διαφορετικές επιλογές για τις παραμέτρους δοκιμάστηκαν για την ταξινόμηση ML. Όσον αφορά τις μήτρες συνδιασποράς τα καλύτερα αποτελέσματα με συνολική cross-validation ακρίβεια του 90,21%±1,11%, λήφθηκαν με τη χρήση των πινάκων συνδιασποράς υπολογισμένων από τα δεδομένα εκπαίδευσης και κανονικοποιώντας τους με την προσθήκη μιας μικρής τιμής c=10-10 στη διαγώνιο. Χρησιμοποιώντας μεγαλύτερες τιμές για c πάντα έδινε καλύτερα αποτελέσματα για τις τάξεις που εκπροσωπούνται από λιγότερα δεδομένα εκπαίδευσης, αλλά υποβάθμιζε τα αποτελέσματα για τις άλλες τάξεις. Η χρήση γραμμικών ορίων απόφασης μέσω ενός κοινού πίνακα συνδιασποράς για όλες τις τάξεις απέδωσε μόνο μια συνολική ακρίβεια του 85,90%±1,35%. Η επιλογή των a priori πιθανοτήτων για τις διαφορετικές υποτάξεις είχαν σημαντική επίδραση στο αποτέλεσμα. Καθώς οι a priori πιθανότητες δόθηκαν μόνο για τις 10 προκαθορισμένες τάξεις (πίνακας 2) και όχι για τις υποτάξεις τους, που λήφθηκαν με μέση μετατόπιση, αυτές οι πιθανότητες έπρεπε να κατανέμονται καταλλήλως στις υποτάξεις. Στο πλαίσιο αυτό, τα καλύτερα στατιστικά αποτελέσματα προέκυψαν σταθμίζοντας την a priori πιθανότητα για την κάθε τάξη με τον σχετικό αριθμό δειγμάτων εκπαίδευσης από την κάθε αντίστοιχη υποτάξη. Για τα στοιχεία μελέτης της Τενερίφης που μας δόθηκαν, η τελευταία προσέγγιση πέτυχε μόνο μια συνολική crossvalidation ακρίβεια του 87,92%±1,23%, σε σύγκριση με το 90,21%±1,11% της πρώτης προσέγγισης. Από την άλλη πλευρά, με ομοιόμορφες a priori πιθανότητες για όλες τις υποτάξεις μια συνολική ακρίβεια του 88,86%±1,7% λήφθηκε.
ICM ταξινόμηση:
Ο αλγόριθμος ICM θα πρέπει να βελτιώσει το αποτέλεσμα της ταξινόμησης του ταξινομητή ML με τη χρήση χωρικού πλαισίου, Ξεκινήσαμε τον ICM με την ταξινόμηση που παρατίθεται στην εικόνα 3 και τον τρέξαμε για 10 επαναλήψεις. Το ενδιαφέρον αποτέλεσμα είναι ότι η crossvalidation ακρίβεια βελτιώθηκε μετά την πρώτη επανάληψη. Μετά τα μέσα διανύσματα και τους πίνακες συνδιασποράς που ξανά υπολογίστηκαν από την προηγούμενη ταξινόμηση, ο αριθμός των σωστά ταξινομημένων pixels μειώνονταν με κάθε διαδοχική επανάληψη, με την κάθε τάξη εδαφοκάλυψης να επηρεάζεται εξίσου. Το πρόβλημα της μείωσης της ακρίβειας μπορεί βεβαίως να παρακαμφθεί με την αποφυγή της επανεκτίμησης των παραμέτρων και με τη χρήση των αρχικών μέσων διανυσμάτων και πινάκων συνδιασποράς που υπολογίζονται από τα δεδομένα εκπαίδευσης σε όλο τον αλγόριθμο. Σε αυτή την περίπτωση, πράγματι, με κάθε επανάληψη μια υψηλότερη ακρίβεια λήφθηκε και ο αλγόριθμος σύγκλινε μετά από μερικά βήματα, με συνολική ακρίβεια περίπου 91%. Παρόλου που ο ICM χρησιμοποιείται στις περισσότερες εφαρμογές, απέχουμε από αυτή τη διαδικασία, καθώς συνήθως χρειάζεται ακριβείς αρχικές εκτιμήσεις των παραμέτρων, για τις οποίες δεν μπορούμε να εγγυηθούμε στην περίπτωση που εξετάζεται στο παρόν έγγραφο. Επιπλέον, τα αποτελέσματα που επιτεύχθηκαν με αυτόν τον τρόπο δεν ήταν οπτικά πειστικά, καθώς εξακολουθούσαν να περιέχουν πολύ θόρυβο. Επομένως, ως συμβιβαστική λύση θα αναλύσουμε τα αποτελέσματα του αλγορίθμου ICM μετά από 5 επαναλήψεις, με αυτών τον τρόπο αποφεύγεται η υπερβολική φθορά, αλλά εξακολουθείται να επιτρέπεται ένα σημαντικό ποσό εξομάλυνσης. Η αντίστοιχη ταξινόμηση παρουσιάζεται στη εικόνα 4, και πάλι τα μαύρα pixels δηλώνουν αυτά τα σημειακά στοιχεία που ανατέθηκαν στην έξω-τάξη. Σε αυτή την περίπτωση, μια συνολική crossvalidation ακρίβεια του 88,55%±1,35% επιτεύχθηκε. Συγκριτικά, η αντίστοιχη ακρίβεια της αρχικής λύσης που λήφθηκε από την ML ήταν 89,18%±1,11%. Παρόλα αυτά, το αποτέλεσμα της ταξινόμησης ICM είναι οπτικά πιο ικανοποιητικό από αυτό της ML, καθώς είναι λιγότερο θορυβώδες. Η σύγκριση του πλήρους πίνακα σύγχυσης για την ICM δίνεται στον πίνακα 4.

SVM ταξινόμηση:
Η προ επεξεργασία των δεδομένων με μέσημετατόπιση δεν βοήθησε την SVM να βρει καλύτερες ταξινομήσεις. Αυτό δεν προκαλεί έκπληξη καθώς, σε αντίθεση με την ML και την ICM, η SVM δεν αναλαμβάνει τις τάξεις που έχουν κατανεμηθεί μονοτροπικά. Ο πίνακας 5 δίνει τον πίνακα σύγχυσης για την SVM που εκπαιδεύεται σε ένα υποσύνολο των crossvalidation στοιχείων εκπαίδευσης και εξετάζεται στα ίδια δεδομένα όπως οι ταξινομητές ML και ICM. Σημειώνεται, ότι στις τάξεις όπου μόνο λίγα δεδομένα εκπαίδευσης είναι διαθέσιμα, η ακρίβεια της ταξινόμησης είναι σοβαρά μειωμένη. Η συνολική ακρίβεια του 93,32%±0.61% είναι απρόσμενα καλή και μάλλον αισιόδοξα προκατειλημμένη: έχουμε πολύ λίγα επίγεια δεδομένα στο χέρι μας και η διακύμανση της τάξης που πάρθηκε από αυτό το δείγμα μπορεί να είναι μικρότερη από την πραγματική διακύμανση εντός των τάξεων. Η εικόνα 5 απεικονίζει μια ταξινόμηση ολόκληρου του νησιού βασισμένη σε 10.000 τυχαία επιλεγμένα διανύσματα. Συγκρίνοντας, αυτό το αποτέλεσμα με την ταξινόμηση ML αμέσως αντιλαμβανόμαστε ότι ο ταξινομητής SVM απλώνει ένα μεγάλο ποσό της τάξης οικισμός κατά μήκος της νοτιοανατολικής ακτής: σε αυτή την περιοχή , τα επίγεια δεδομένα είναι σπάνια έτσι ο SVM αποφασίζει για τον οικισμό. Επίσης, ο ML λανθασμένα ανιχνεύει οικισμό κατά μήκος της νοτιοανατολικής ακτής, αλλά καθώς ο ML αξιοποιεί a priori τις πληροφορίες για τις πιθανότητες τάξης, κατατάσσει το μεγαλύτερο μέρος της αταξινόμητης περιοχής στην τάξη Cardonal&Tabaibal η οποία είναι ίσως η σωστή ταξινόμηση.
Συμπεράσματα
Σε αυτή την εργασία εφαρμόσαμε τρεις διαφορετικούς αλγόριθμους επιβλεπόμενης ταξινόμησης για να βρούμε μία ετικέτα για μια σχετικά μεγάλη περιοχή, στις προηγουμένως καθορισμένες τάξεις εδαφοκάλυψης. Παρά το γεγονός ότι μόνο λίγα δεδομένα εκπαίδευσης ήταν διαθέσιμα, οι crossvalidation δοκιμές αποκάλυψαν μια υψηλή ακρίβεια ταξινόμησης για όλους τους ταξινομητές. Αλλά τα στατιστικά αποτελέσματα μπορεί να είναι παραπλανητικά: αν και ο SVM συγκεντρώνει τη μεγαλύτερη ακρίβεια, η οπτική εντύπωση δεν είναι τόσο ικανοποιητική όσο το αποτέλεσμα του ML γιατί πολλά pixels χαρακτηρίστηκαν ως οικισμός. Στο πλαίσιο αυτό, είναι βασικό πλεονέκτημα του ML ότι οι a priori πληροφορίες για τις πιθανότητες των τάξεων μπορούν να ενσωματωθούν πολύ εύκολα, έτσι ώστε οι απίθανες τάξεις καταστέλλονται στη τελική ταξινόμηση. Σε αυτή την κατεύθυνση, συνδυάζοντας τον SVM με έναν εξειδικευμένο παραμετρικό ταξινομητή όπως ο ICM, ο οποίος είναι ικανός να χρησιμοποιεί a priori πιθανότητες και να εξομαλύνει τη θορυβώδη ταξινόμηση, θα ήταν μια χρήσιμη βελτίωση. Εκμεταλλεύοντας το χωρικό πλαίσιο, εφαρμόζοντας τον ICM στο αποτέλεσμα μιας ML ταξινόμησης ήταν ευεργετικό: μια πολύ πιο ομαλή ταξινόμηση επιτεύχθηκε. Αλλά, η σποραδικότητα των δεδομένων εκπαίδευσης οδηγεί σε κατατμήσεις οι οποίες στατιστικά μειώνονται σε ακρίβεια με κάθε επανάληψη. Έτσι, διαχειρίζοντας μικτά pixels πιο σωστά μπορεί να παίξει σημαντικό ρόλο για την επίτευξη καλύτερων αποτελεσμάτων. Αντί της σκληρής ταξινόμησης του κάθε pixel, μπορεί κάποιος να χρησιμοποιήσει ασαφείς ετικετοποιήσεις κατά τη διάρκεια του ICM, το οποίο επιτρέπει στο σημειακό δεδομένο να έχει μερική συμμετοχή στην τάξη. Για την Τενερίφη, η συμπερίληψη των τιμών υψομέτρου ως πρόσθετο κανάλι εισόδου βελτίωσε τα αποτελέσματα της ταξινόμησης, καθώς μερικές τάξεις περιορίστηκαν αποτελεσματικά στο σωστό εύρος υψομέτρου. Για την ταξινόμηση ML, η υπόθεση μιας μονοτροπικής Γκαουσιανής κατανομής δεν είναι πάντα σωστή. Η προ επεξεργασία των δεδομένων εκπαίδευσης με τον αλγόριθμο μέσηςμετατόπισης ήταν πολύ χρήσιμη. Ωστόσο, στις περιπτώσεις όπου η βασική υπόθεση σχετικά με την μορφή της κατανομής παραβιάζεται πολύ έντονα, η χρήση ενός μη παραμετρικού ταξινομητή όπως ο SVM μπορεί να είναι πιο κατάλληλη.