Επιβλεπόμενη Ταξινόμηση της Γεωργικής κάλυψης εδάφους με χρήση μιας Τροποποιημένης k-NN Τεχνικής (ΜΝΝ) και Landsat τηλεπισκοπικών εικόνων
Από RemoteSensing Wiki
| Γραμμή 40: | Γραμμή 40: | ||
<b>Αποτελέσματα</b><br> | <b>Αποτελέσματα</b><br> | ||
| - | Η ισχύς και η αξιοπιστία της μεθόδου ΜΝΝ εκτιμήθηκε με την πρότυπη προσέγγιση του πίνακα σύγχυσης. Το σχήμα 2 | + | Η ισχύς και η αξιοπιστία της μεθόδου ΜΝΝ εκτιμήθηκε με την πρότυπη προσέγγιση του πίνακα σύγχυσης. Το σχήμα 2 απεικονίζει την ισχύ της προτεινόμενης προσέγγισης σε σύγκριση με τις μεθόδους ML και k-NN χρησιμοποιώντας την πρότυπη Ευκλείδεια απόσταση στο διάστημα πρόβλεψης. Τα αποτελέσματα της προσομοίωσης δείχνουν ότι η μέση ολική ακρίβεια που λαμβάνεται για την ΜΝΝ είναι ακόμη μεγαλύτερη και από το ανώτερο όριο εμπιστοσύνης 95% των αποτελεσμάτων που προκύπτουν από την μέθοδο ML. Το πρότυπο k-ΝΝ (χωρίς κάποιον μετασχηματισμό) έχει χαμηλή επίδοση σε όλα αυτά τα ανεξάρτητα δείγματα. |
[[Εικόνα:Stlas_knn_4_02.jpg|right|thumb||Σχήμα 2 : Γράφημα που δείχνει τη μεταβολή του διαστήματος εμπιστοσύνης 90%, ανάλογα με τον αριθμό των εγγύτερων γειτόνων, καθώς και το διάστημα εμπιστοσύνης για τις μεθόδους ML και k-NN. [http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=4539262]πηγή]] | [[Εικόνα:Stlas_knn_4_02.jpg|right|thumb||Σχήμα 2 : Γράφημα που δείχνει τη μεταβολή του διαστήματος εμπιστοσύνης 90%, ανάλογα με τον αριθμό των εγγύτερων γειτόνων, καθώς και το διάστημα εμπιστοσύνης για τις μεθόδους ML και k-NN. [http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=4539262]πηγή]] | ||
| - | Επίσης ερευνήσαμε, πώς η επιλογή των μεταβλητών επηρεάζει την αποδοτικότητα των διαφορετικών μεθόδων. Με βάση το σχήμα | + | Επίσης ερευνήσαμε, πώς η επιλογή των μεταβλητών επηρεάζει την αποδοτικότητα των διαφορετικών μεθόδων. Με βάση το σχήμα 3 μπορούμε να συμπεράνουμε ότι οι επιβλεπόμενες ταξινομήσεις των πολύ-χρονικών σκηνών παρέχουν καλύτερα αποτελέσματα από εκείνα των μονό-χρονικών. Ένα ακόμη αποτέλεσμα που προέρχεται από αυτά τα πειράματα είναι ότι η μέθοδος ΜΝΝ αποδίδει πολύ καλύτερα από την μέθοδο ML(μεγίστης πιθανοφάνειας) όταν το μέγεθος του δείγματος ανά τάξη είναι μικρό. Αυτό είναι ένα πλεονέκτημα διότι μειώνει το κόστος της συλλογής των δεδομένων, χωρίς να τίθεται σε κίνδυνο η ποιότητα των αποτελεσμάτων. |
Με βάση τα αποτελέσματα της ανάλυσης ευαισθησίας, η τελική ταξινόμηση όλης της περιοχής δοκιμών πραγματοποιήθηκε με τη χρήση πολύ-χρονικών δεδομένων ενσωματωμένα σε ένα τρισδιάστατο χώρο και με τη χρήση Ν=5 γειτόνων. | Με βάση τα αποτελέσματα της ανάλυσης ευαισθησίας, η τελική ταξινόμηση όλης της περιοχής δοκιμών πραγματοποιήθηκε με τη χρήση πολύ-χρονικών δεδομένων ενσωματωμένα σε ένα τρισδιάστατο χώρο και με τη χρήση Ν=5 γειτόνων. | ||
[[Εικόνα:Stlas_knn_5_02.jpg|right|thumb||Σχήμα 3 : Γραφική παράσταση που δείχνει την επιρροή του μεγέθους του δείγματος ανά τάξη στην ολική ακρίβεια της ταξινόμησης.[http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=4539262]πηγή]] | [[Εικόνα:Stlas_knn_5_02.jpg|right|thumb||Σχήμα 3 : Γραφική παράσταση που δείχνει την επιρροή του μεγέθους του δείγματος ανά τάξη στην ολική ακρίβεια της ταξινόμησης.[http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=4539262]πηγή]] | ||
Αναθεώρηση της 16:55, 25 Ιανουαρίου 2012
Επιβλεπόμενη Ταξινόμηση της Γεωργικής κάλυψης εδάφους με χρήση μιας Τροποποιημένης k-NN Τεχνικής (ΜΝΝ) και Landsat τηλεπισκοπικών εικόνων
Supervised Classification of Agricultural Land Cover Using a Modified k-NN Technique (MNN) and Landsat Remote Sensing Imagery Luis Samaniego, András Bárdossy, Karsten Schulz IEEE Transactions on Geoscience and Remote Sensing (2008) Volume: 46, Issue: 7, Publisher: IEEE, Pages: 2112-2125 [8]
Περίληψη
Οι τεχνικές του Εγγύτερου Γείτονα χρησιμοποιούνται συχνά στην Τηλεπισκόπηση, την αναγνώριση προτύπων και τις στατιστικές, για την ταξινόμηση αντικειμένων σε ένα προκαθορισμένο αριθμό κατηγοριών βασισμένες σε ένα δεδομένο σύνολο προβλέψεων . Αυτές οι τεχνικές είναι ιδιαίτερα χρήσιμες για την μη γραμμική σχέση μεταξύ των μεταβλητών.. Στις περισσότερες μελέτες το μέτρο της απόστασης υιοθετείται εκ των προτέρων. Αντίθετα προτείνουμε μια γενική διαδικασία για την εύρεση μιας προσαρμοστικής μέτρησης που συνδυάζει μια τεχνική τοπικής μείωσης της διασποράς και μια γραμμική ενσωμάτωση του διαστήματος παρατήρησης σε ένα κατάλληλο Ευκλείδειο διάστημα. Για να επεξηγηθεί η εφαρμογή αυτής της τεχνικής παρουσιάζονται δυο ταξινομήσεις γεωργικής εδαφοκάλυψης με χρήση μονό-χρονικών και πολύ-χρονικών σκηνών Landsat. Τα αποτελέσματα της μελέτης, σε σύγκριση με τις συνήθεις προσεγγίσεις που χρησιμοποιούνται στην Τηλεπισκόπηση όπως της Μεγίστης Πιθανοφάνειας (ML) ή k-Εγγύτερου Γείτονα (k-ΝΝ) δείχνουν ουσιαστική βελτίωση όσον αφόρα την γενική ακρίβεια και την πληθικότητα του συνόλου των δεδομένων βαθμονόμησης.
Εισαγωγή
Η τηλεπισκόπηση έχει γίνει ένα σημαντικό εργαλείο στους ευρείς τομείς της περιβαλλοντικής έρευνας και σχεδιασμού. Ειδικότερα η ταξινόμηση των φασματικών εικόνων είναι μια επιτυχής εφαρμογή που χρησιμοποιείται για την παραγωγή χαρτών κάλυψης εδάφους, την αξιολόγηση της αποδάσωσης και των καμένων δασικών περιοχών, την πυρανίχνευση σε πραγματικό χρόνο, την εκτίμηση της επιφάνειας των καλλιεργειών και της παραγωγής ή τον έλεγχο της περιβαλλοντικής ρύπανσης. Επίσης η ταξινόμηση εικόνας εφαρμόζεται αρκετά συχνά και σε άλλα πλαίσια, όπως η οπτική αναγνώριση προτύπων και αντικειμένων στις ιατρικές ή άλλες βιομηχανικές διαδικασίες. Κατά συνέπεια, διάφοροι αλγόριθμοι για την Επιβλεπόμενη Ταξινόμηση έχουν αναπτυχθεί τελευταία για να αντιμετωπίσουν τόσο την αυξανόμενη ζήτηση αυτών των προϊόντων, όσο και τα ειδικά χαρακτηριστικά ποικίλων επιστημονικών προβλημάτων. Τα παραδείγματα περιλαμβάνουν την μέθοδο Μεγίστης Πιθανοφάνειας, τις τεχνικές βασισμένες στον συγκεχυμένο-κανόνα, την Bayesian και τεχνητά νευρωνικά δίκτυα, τις διανυσματικές μηχανές υποστήριξης και την τεχνική του k-Εγγύτερου Γείτονα (k-NN). Σε γενικές γραμμές ένας αλγόριθμος επιβλεπόμενης ταξινόμησης μπορεί να υποδιαιρεθεί σε δυο φάσεις, (1) η εκμάθηση ή “βαθμονόμηση” φάση κατά την οποία ο αλγόριθμος προσδιορίζει ένα σχέδιο ταξινόμησης βασισμένο στις φασματικές υπογραφές των διαφορετικών καναλιών που λαμβάνονται από τις περιοχές εκπαίδευσης, ξέροντας τις ετικέτες των τάξεων(π.χ. κάλυψη εδάφους ή τύπο καλλιεργειών) και (2) η φάση πρόβλεψης, κατά την οποία το σχέδιο ταξινόμησης εφαρμόζεται σε άλλες θέσεις με άγνωστη την ιδιότητα του μέλους της τάξης. Οι αλγόριθμοι που προαναφερθήκαν ακολουθούν το παραδοσιακό παράδειγμα διαμόρφωσης που προσπαθεί να βρει το «βέλτιστο» σύνολο παραμέτρων το οποίο κλείνει την απόσταση μεταξύ των παρατηρούμενων χαρακτηριστικών και του αποτελέσματος της ταξινόμησης. Μια κάπως διαφορετική προσέγγιση έχει πρόσφατα προταθεί, ως η τροποποιημένη τεχνική Εγγύτερου Γείτονα μέσα στα πλαίσια της ταξινόμησης κάλυψης εδάφους σε ένα έργο υδρολογικής διαμόρφωσης μέσης κλίμακας. Ο αλγόριθμος ΜΝΝ είναι ένας υβριδικός αλγόριθμος που συνδυάζει τα χαρακτηριστικά ενός αλγορίθμου μείωσης διαστατικότητας και τα πλεονεκτήματα του προτύπου k-ΝΝ που είναι : (1) μια εξαιρετικά ευέλικτη τεχνική επιβλεπόμενης ταξινόμησης, η οποία απαιτεί μόνο μια παράμετρο (k ο αριθμός του εγγύτερου γείτονα), (2) εξαιρετικά ελκυστική για λειτουργικούς λόγους διότι, ούτε απαιτεί την προεπεξεργασία των δεδομένων, ούτε παραδοχές όσον αφορά την κατανομή των δεδομένων εκπαίδευσης και (3) μια αρκετά ισχυρή τεχνική, διότι ο ενιαίος κανόνας 1-ΝΝ εγγυάται ένα ασυμπτωτικό ποσοστό σφάλματος το πολύ διπλάσιο από αυτό της πιθανότητας σφάλματος Bayes. Ωστόσο, η τεχνική k-ΝΝ έχει και αρκετές αδυναμίες που έχουν ήδη εξετασθεί στη βιβλιογραφία. Για παράδειγμα, (1) η απόδοση της εξαρτάται ιδιαίτερα από την επιλογή του k, (2) η συγκέντρωση εγγύτερων γειτόνων από τα δεδομένα εκπαίδευσης που περιέχουν επικαλυπτόμενες τάξεις θεωρείται ακατάλληλη, (3) η αποκαλούμενη “κατάρα “ της διαστατικότητας μπορεί να βλάψει σοβαρά την απόδοση της στα πεπερασμένα δείγματα και τέλος (4) η επιλογή της μετρικής απόστασης είναι κρίσιμη για να καθορίσει την έκβαση της ταξινόμησης του εγγύτερου γείτονα. Προκείμενου να ξεπεραστούν αυτές οι ελλείψεις ή τουλάχιστον μέρος αυτών, η τεχνική ΜΝΝ εγκαταλείπει το παραδοσιακό παράδειγμα διαμόρφωσης που προσπαθεί να βρει το «βέλτιστο» σύνολο παραμέτρων το οποίο κλείνει την απόσταση μεταξύ των παρατηρούμενων χαρακτηριστικών και του αποτελέσματος της ταξινόμησης. Από την άλλη, ένας μετασχηματισμός του αρχικού χαρακτηριστικού διαστήματος επιλέγεται με τέτοιο τρόπο ώστε οι παρατηρήσεις που μοιράζονται μια δεδομένη ετικέτα κατηγορίας (είδος καλλιέργειας) είναι πολύ πιθανό να ταξινομηθούν μαζί, ενώ οι υπόλοιπες τείνουν να απομακρύνονται όλο και περισσότερο. Η μέθοδος ΜΝΝ έχει εισαχθεί μέσα σε μια μέσης κλίμακας υδρολογική εφαρμογή, όπου μια σκηνή Landsat έχει χρησιμοποιηθεί για να παράγει ένα χάρτη κάλυψης εδάφους 3 τάξεων ( δάσος, διαπερατό, μη διαπερατό) της περιοχής Upper Neckar στη Γερμανία. Η μέθοδος ΜΝΝ έχει επίσης συγκριθεί εκτενώς με άλλες μεθόδους ταξινόμησης και έδειξε υψηλές αποδόσεις. Παρακάτω ακολουθεί ανάλυση της μεθόδου ΜΝΝ και επίδειξη της απόδοσης της σε ένα πρόβλημα ταξινόμησης γεωργικής χρήσης γης σε περιοχή της Γερμανίας με τη χρήση μόνο-χρονικών και πολύ-χρονικών σκηνών Landsat.
Η μέθοδος ΜΝΝ
Ένα πολύ σημαντικό χαρακτηριστικό της προτεινόμενης τεχνικής ΜΝΝ έναντι των συμβατικών προσεγγίσεων ΝΝ (εγγύτερου γείτονα) είναι ο τρόπος με τον οποίο υπολογίζονται οι αποστάσεις μεταξύ των παρατηρήσεων. Οι μέθοδοι ΝΝ απαιτούν τον α priori καθορισμό μιας απόστασης ή χ – διάστημα. Επειδή η επιλογή της απόστασης επηρεάζει την απόδοση του αλγορίθμου ταξινόμησης, συνήθως εξετάζονται ποικίλες λογικές αποστάσεις, παραδείγματος χάριν: το πρότυπο L1 (ή απόσταση Μανχάταν), το πρότυπο L2 (ή Ευκλείδεια απόσταση), το πρότυπο L1 (ή απόσταση Chebycher), η απόσταση Mahalanobis και τα μέτρα ομοιότητας όπως η Pearson και η συσχέτιση Spearman-Rank. Στην τεχνική ΜΝΝ αντίθετα, ψάχνουμε για μια μέτρηση σε μικρότερων διαστάσεων χώρο ή την ενσωμάτωση του διαστήματος που είναι κατάλληλο για το διαχωρισμό μιας δεδομένης τάξης. Στην ουσία η μέθοδος ΜΝΝ βρίσκει έναν μη γραμμικό μετασχηματισμό (ή τη χαρτογράφηση) που ελαχιστοποιεί την μεταβλητότητα ενός δεδομένου μέλους της τάξης, όλων αυτών των ζευγών σημείων των οποίων η συσσωρευτική απόσταση είναι μικρότερη από μια προκαθορισμένη τιμή (D). Αξίζει να σημειωθεί ότι ο όρος αυτός δεν συνεπάγεται την εύρεση συσσωρεύσεων στον προβλεπόμενο χώρο που ελαχιστοποιούν τη συνολική ενδό-ομαδική διακύμανση, η οποία είναι συνηθισμένη προϋπόθεση στην ανάλυση των συσσωρεύσεων. Ένας μικρότερων διαστάσεων χώρος ενσωμάτωσης προτιμάται στην μέθοδο ΜΝΝ, εάν είναι δυνατόν, λόγω των εμπειρικών στοιχείων που υποστηρίζουν το γεγονός ότι η εγγενής πολλαπλή διάσταση των πολυμεταβλητών δεδομένων είναι σημαντικά μικρότερη από αυτή των δεδομένων εισόδου. Ένας απλός τρόπος για να επαληθευτεί αυτή η υπόθεση είναι ο υπολογισμός της διάστασης του πίνακα συνδιασποράς των τυποποιημένων προβλέψεων και να μετρηθεί ο αριθμός των κυρίαρχων ιδιοδιανυσμάτων. Εν ολίγοις, αυτή η μέθοδος επιδιώκει διαφορετικές μετρήσεις, μια για κάθε τάξη h, στα αντίστοιχα διαστήματα ενσωμάτωσης τους, που καθορίζονται από τους μετασχηματισμούς Bh, έτσι ώστε η συσσωρευτική διαφορά των ιδιοτήτων της τάξης για μια δεδομένη μερίδα των πλησιέστερων ζευγών παρατηρήσεων να ελαχιστοποιείται. Συνεπώς αυτές οι μετρήσεις δεν είναι σφαιρικές.
Εφαρμογές
Η προτεινόμενη μέθοδος εφαρμόστηκε σε δύο διαφορετικά παραδείγματα ταξινόμησης κάλυψης εδάφους, χρησιμοποιώντας 1) μεμονωμένες και 2) πολύ-χρονικές εικόνες Landsat TM/ETM+ για το έτος 1999. Και τα δύο παραδείγματα χρησιμοποιούν δεδομένα από γεωργικές περιοχές δοκιμής που βρίσκονται στην Parthe-λεκάνη νοτιοανατολικά της Λειψίας, Γερμανία. Η περιοχή μελέτης είναι μέρος του γερμανικού συγκροτήματος-loess που αποτελείται από ιδιαίτερα παραγωγικά εδάφη με την χρήση γης να κυριαρχείται από γεωργικές δραστηριότητες.

Οι περιοχές δοκιμής περιλαμβάνουν 23 πεδία με συνολική έκταση 426 εκτάρια. Οι κύριοι τύποι εδάφους είναι Cambisol, Luvisol και Stagnic Gleysol και κυριαρχούν χειμώνα, καλοκαίρι οι καλλιέργειες σιτηρών, με συνολικό ποσοστό άνω του 70%.
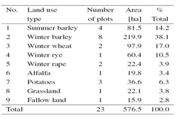
Επιπλέον, 3 εικόνες Landsat της περιοχής μελέτης έχουν διατεθεί για την αγροτική περίοδο του 1999 : 2 Landsat 5-TM σκηνές από τις 30 Απριλίου και 3 Ιουλίου (διαδρομή/σειρά 193/025) και μια σκηνή Landsat 7-ETM+ από τις 13 Σεπτεμβρίου 1999 (διαδρομή/σειρά 193/024). Και οι τρεις εικόνες γεω-αναφερθήκαν στο λογισμικό ERDAS imagine χρησιμοποιώντας ένα ψηφιακό τοπογραφικό χάρτη σε κλίμακα 1:25000 και 40 μεγάλης βαρύτητας σημεία αναφοράς, με αποτέλεσμα ένα μέγιστο RMSE- σφάλμα της τάξης των 7.8m. Και για τα δυο παραδείγματα χρησιμοποιήσαμε μόνο τα 6 κανάλια στην περιοχή του ορατού και του εγγύς υπέρυθρου, αγνοώντας κατά συνέπεια τα θερμικά κανάλια του ΤΜ και ΕΤΜ+, καθώς και το παγχρωματικό κανάλι του ΕΤΜ+. Σημειώνεται ότι ατμοσφαιρική διόρθωση δεν έχει γίνει.

Αποτελέσματα
Η ισχύς και η αξιοπιστία της μεθόδου ΜΝΝ εκτιμήθηκε με την πρότυπη προσέγγιση του πίνακα σύγχυσης. Το σχήμα 2 απεικονίζει την ισχύ της προτεινόμενης προσέγγισης σε σύγκριση με τις μεθόδους ML και k-NN χρησιμοποιώντας την πρότυπη Ευκλείδεια απόσταση στο διάστημα πρόβλεψης. Τα αποτελέσματα της προσομοίωσης δείχνουν ότι η μέση ολική ακρίβεια που λαμβάνεται για την ΜΝΝ είναι ακόμη μεγαλύτερη και από το ανώτερο όριο εμπιστοσύνης 95% των αποτελεσμάτων που προκύπτουν από την μέθοδο ML. Το πρότυπο k-ΝΝ (χωρίς κάποιον μετασχηματισμό) έχει χαμηλή επίδοση σε όλα αυτά τα ανεξάρτητα δείγματα.

Επίσης ερευνήσαμε, πώς η επιλογή των μεταβλητών επηρεάζει την αποδοτικότητα των διαφορετικών μεθόδων. Με βάση το σχήμα 3 μπορούμε να συμπεράνουμε ότι οι επιβλεπόμενες ταξινομήσεις των πολύ-χρονικών σκηνών παρέχουν καλύτερα αποτελέσματα από εκείνα των μονό-χρονικών. Ένα ακόμη αποτέλεσμα που προέρχεται από αυτά τα πειράματα είναι ότι η μέθοδος ΜΝΝ αποδίδει πολύ καλύτερα από την μέθοδο ML(μεγίστης πιθανοφάνειας) όταν το μέγεθος του δείγματος ανά τάξη είναι μικρό. Αυτό είναι ένα πλεονέκτημα διότι μειώνει το κόστος της συλλογής των δεδομένων, χωρίς να τίθεται σε κίνδυνο η ποιότητα των αποτελεσμάτων. Με βάση τα αποτελέσματα της ανάλυσης ευαισθησίας, η τελική ταξινόμηση όλης της περιοχής δοκιμών πραγματοποιήθηκε με τη χρήση πολύ-χρονικών δεδομένων ενσωματωμένα σε ένα τρισδιάστατο χώρο και με τη χρήση Ν=5 γειτόνων.



Συμπεράσματα
Από τα παραπάνω φαίνεται πως η μέθοδος ΜΝΝ αποδίδει πολύ καλύτερα από τις δύο άλλες μεθόδους, την Μεγίστης Πιθανοφάνειας ML και την πρότυπη μέθοδο k-NN σε όλες τις εξεταζόμενες περιπτώσεις. Επίσης επιβεβαιώθηκε και το πλεονέκτημα της χρήσης πολύ-χρονικών δεδομένων για την μέθοδο ΜΝΝ. Ένα ακόμη πλεονέκτημα της μεθόδου είναι η μικρή της ευαισθησία στον αριθμό των δεδομένων του συνόλου κατάρτισης, που οδηγεί σε μια ισχυρή και οικονομικώς αποδοτική βαθμονόμηση του προβλήματος ταξινόμησης. Ωστόσο, πριν γίνει λειτουργική κάποιες περαιτέρω πτυχές της μεθόδου πρέπει ακόμη να ερευνηθούν. Η τεχνική ΜΝΝ μπορεί να βελτιωθεί με την εξέταση των μη γραμμικών μετασχηματισμών και/ή με την κατάλληλη διατύπωση για τις παραλλαγές της μέσα στο διάστημα παρατήρησης. Ενώ, όντας πέρα από το πεδίο αυτού του εγγράφου, αυτές οι πτυχές θα κατευθύνουν τις μελλοντικές ερευνητικές δραστηριότητες μας και θα παρουσιαστούν στο εγγύς μέλλον.