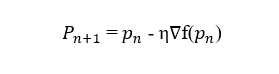Gradient Descent (Κλίση Καθόδου)
Από RemoteSensing Wiki
(Νέα σελίδα με ''''Gradient Descent''' '''<span style="color:#006400"> Εισαγωγή </span>''' Η κλίση καθόδου (gradie...') |
|||
| Γραμμή 13: | Γραμμή 13: | ||
Ο όρος «κλίση» αναφέρεται στο μέτρο της μεταβολής όλων των βαρών ενός μοντέλου ως αποτέλεσμα της μεταβολής του σφάλματος. Μπορούμε επίσης να σκεφτούμε την κλίση ως την κλίση μιας συνάρτησης. Όσο μεγαλύτερη είναι η κλίση, τόσο πιο απότομη είναι η κάθοδος και τόσο γρηγορότερα μαθαίνει ένα μοντέλο. Αν όμως η κλίση είναι μηδενική, το μοντέλο σταματά να μαθαίνει. Μαθηματικά, η κλίση είναι μια μερική παράγωγος ως προς τις εισόδους της. | Ο όρος «κλίση» αναφέρεται στο μέτρο της μεταβολής όλων των βαρών ενός μοντέλου ως αποτέλεσμα της μεταβολής του σφάλματος. Μπορούμε επίσης να σκεφτούμε την κλίση ως την κλίση μιας συνάρτησης. Όσο μεγαλύτερη είναι η κλίση, τόσο πιο απότομη είναι η κάθοδος και τόσο γρηγορότερα μαθαίνει ένα μοντέλο. Αν όμως η κλίση είναι μηδενική, το μοντέλο σταματά να μαθαίνει. Μαθηματικά, η κλίση είναι μια μερική παράγωγος ως προς τις εισόδους της. | ||
| - | Ένα απτό παράδειγμα είναι το εξής: Ένας τυφλός άνθρωπος θέλει να ανέβει στην κορυφή ενός λόφου με τον λιγότερο δυνατό αριθμό βημάτων. Αρχικά, μπορεί να αρχίσει να ανεβαίνει το λόφο κάνοντας πολύ μεγάλα βήματα προς την πιο απότομη κατεύθυνση, όσο δεν είναι κοντά στην κορυφή. Καθώς πλησιάζει όμως στην κορυφή, τα βήματά του γίνονται ολοένα και μικρότερα για να αποφύγει το να την υπερβεί. Αυτή η διαδικασία μπορεί να περιγραφεί μαθηματικά χρησιμοποιώντας την έννοια της κλίσης[1]. | + | Ένα απτό παράδειγμα είναι το εξής: Ένας τυφλός άνθρωπος θέλει να ανέβει στην κορυφή ενός λόφου με τον λιγότερο δυνατό αριθμό βημάτων. Αρχικά, μπορεί να αρχίσει να ανεβαίνει το λόφο κάνοντας πολύ μεγάλα βήματα προς την πιο απότομη κατεύθυνση, όσο δεν είναι κοντά στην κορυφή. Καθώς πλησιάζει όμως στην κορυφή, τα βήματά του γίνονται ολοένα και μικρότερα για να αποφύγει το να την υπερβεί. Αυτή η διαδικασία μπορεί να περιγραφεί μαθηματικά χρησιμοποιώντας την έννοια της κλίσης [1]. |
| Γραμμή 38: | Γραμμή 38: | ||
Η εφαρμογή της κλίσης καθόδου είναι ευρέως διαδεδομένη σε προβλήματα μηχανικής μάθησης. | Η εφαρμογή της κλίσης καθόδου είναι ευρέως διαδεδομένη σε προβλήματα μηχανικής μάθησης. | ||
| + | |||
1. '''Εκπαίδευση Νευρωνικών Δικτύων (Neural Networks):''' | 1. '''Εκπαίδευση Νευρωνικών Δικτύων (Neural Networks):''' | ||
| - | Τα νευρωνικά δίκτυα χρησιμοποιούνται ευρέως σε προβλήματα μηχανικής μάθησης, όπως αναγνώριση εικόνας, φωνής, και άλλα. Κατά τη διάρκεια της εκπαίδευσης των νευρωνικών δικτύων, η κλίση καθόδου χρησιμοποιείται για την ενημέρωση των βαρών του δικτύου με σκοπό την ελαχιστοποίηση της συνάρτησης κόστους[2]. | + | Τα νευρωνικά δίκτυα χρησιμοποιούνται ευρέως σε προβλήματα μηχανικής μάθησης, όπως αναγνώριση εικόνας, φωνής, και άλλα. Κατά τη διάρκεια της εκπαίδευσης των νευρωνικών δικτύων, η κλίση καθόδου χρησιμοποιείται για την ενημέρωση των βαρών του δικτύου με σκοπό την ελαχιστοποίηση της συνάρτησης κόστους [2]. |
2. '''Γραμμική Κατηγοριοποίηση και Παλινδρόμηση: ''' | 2. '''Γραμμική Κατηγοριοποίηση και Παλινδρόμηση: ''' | ||
| - | Σε αλγόριθμους παλινδρόμησης και κατηγοριοποίησης, όπως η γραμμική παλινδρόμηση και η λογιστική παλινδρόμηση, η κλίση καθόδου χρησιμοποιείται για την εκπαίδευση του μοντέλου προσαρμόζοντας τις παραμέτρους προς την κατεύθυνση της ελαχιστοποίησης του κόστους[3]. | + | Σε αλγόριθμους παλινδρόμησης και κατηγοριοποίησης, όπως η γραμμική παλινδρόμηση και η λογιστική παλινδρόμηση, η κλίση καθόδου χρησιμοποιείται για την εκπαίδευση του μοντέλου προσαρμόζοντας τις παραμέτρους προς την κατεύθυνση της ελαχιστοποίησης του κόστους [3]. |
3. '''Μηχανή Διανυσματικής Υποστήριξης (SVM): ''' | 3. '''Μηχανή Διανυσματικής Υποστήριξης (SVM): ''' | ||
| - | Η κλίση καθόδου χρησιμοποιείται για την εκπαίδευση μοντέλων SVM προσαρμόζοντας τις παραμέτρους τους για την επίτευξη βέλτιστης απόστασης μεταξύ των κλάσεων[4]. | + | Η κλίση καθόδου χρησιμοποιείται για την εκπαίδευση μοντέλων SVM προσαρμόζοντας τις παραμέτρους τους για την επίτευξη βέλτιστης απόστασης μεταξύ των κλάσεων [4]. |
4. '''Βελτιστοποίηση Υπερπαραμέτρων:''' | 4. '''Βελτιστοποίηση Υπερπαραμέτρων:''' | ||
| Γραμμή 74: | Γραμμή 75: | ||
5. '''Επανάληψη:''' Επαναλαμβάνουμε τη διαδικασία για πολλές εποχές (epochs), προσπαθώντας να μειώσουμε συνεχώς το σφάλμα. | 5. '''Επανάληψη:''' Επαναλαμβάνουμε τη διαδικασία για πολλές εποχές (epochs), προσπαθώντας να μειώσουμε συνεχώς το σφάλμα. | ||
| + | |||
• '''Mini-Batch Gradient Descent: ''' | • '''Mini-Batch Gradient Descent: ''' | ||
| - | Ο Mini-batch gradient descent συνδυάζει ιδέες από τους αλγορίθμους batch gradient descent και στοχαστικής κλίσης καθόδου. Διαιρεί τα σετ δεδομένων εκπαίδευσης σε μικρά τμήματα (μικρές δέσμες) και κάνει ενημερώσεις(updates) σε κάθε δέσμη. Αυτή η προσέγγιση εξασφαλίζει μια ισορροπία ανάμεσα στην αποτελεσματικότητα του batch gradient descent και την ταχύτητα της στοχαστικής κλίσης καθόδου[6]. | + | Ο Mini-batch gradient descent συνδυάζει ιδέες από τους αλγορίθμους batch gradient descent και στοχαστικής κλίσης καθόδου. Διαιρεί τα σετ δεδομένων εκπαίδευσης σε μικρά τμήματα (μικρές δέσμες) και κάνει ενημερώσεις(updates) σε κάθε δέσμη. Αυτή η προσέγγιση εξασφαλίζει μια ισορροπία ανάμεσα στην αποτελεσματικότητα του batch gradient descent και την ταχύτητα της στοχαστικής κλίσης καθόδου [6]. |
Παρούσα αναθεώρηση της 10:39, 31 Ιανουαρίου 2024
Εισαγωγή
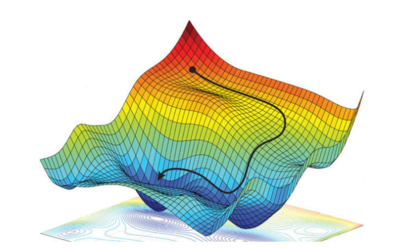
Η κλίση καθόδου (gradient descent) έχει αναδειχθεί ως ένα αποτελεσματικό εργαλείο βελτιστοποίησης με ευρεία εφαρμογή σε πολλούς αλγορίθμους μηχανικής μάθησης, συμπεριλαμβανομένων των νευρωνικών δικτύων. Ο βασικός σκοπός αυτού του αλγορίθμου βελτιστοποίησης είναι η ελαχιστοποίηση μιας κυρτής συνάρτησης κόστους, η οποία αντιπροσωπεύει την απόδοση ενός μοντέλου. Η βασική ιδέα πίσω από την κλίση καθόδου είναι να προσαρμόζονται επαναληπτικά οι παράμετροι ενός μοντέλου με στόχο την ελαχιστοποίηση της συνάρτησης κόστους. Κατά τη διαδικασία αυτή, οι παράμετροι ενημερώνονται με βάση την αντίθετη κατεύθυνση της κλίσης της συνάρτησης κόστους. Αυτό σημαίνει ότι το μοντέλο κινείται προς την κατεύθυνση της μεγαλύτερης αύξησης της συνάρτησης κόστους, με σκοπό την εύρεση του ελάχιστου. Ουσιαστικά, η διαδικασία είναι ως εξής: Αφού προσδιοριστεί μια αρχική θέση (ή σύνολο παραμέτρων) για το μοντέλο, η κλίση της συνάρτησης κόστους υπολογίζεται σε αυτήν τη θέση. Στη συνέχεια, οι παράμετροι ενημερώνονται κατά μήκος της αντίθετης κατεύθυνσης της κλίσης, λαμβάνοντας υπόψιν έναν ρυθμό εκμάθησης. Αυτή η διαδικασία επαναλαμβάνεται μέχρις ότου επιτευχθεί σύγκλιση σε ένα ολικό ελάχιστο. Είναι σημαντικό να τονίσουμε ότι η αποτελεσματικότητα της κλίσης καθόδου οφείλεται στο γεγονός ότι οι περισσότερες συναρτήσεις κόστους είναι κυρτές. Αυτό εξασφαλίζει την σύγκλιση του αλγορίθμου σε ένα ολικό ελάχιστο. Η κλίση καθόδου αντιπροσωπεύει ένα βασικό κομμάτι της εφαρμογής μηχανικής μάθησης, επιτρέποντας τη βελτιστοποίηση μοντέλων και την προσαρμογή τους προς τα επιθυμητά αποτελέσματα.
Τι είναι κλίση (gradient);
Ο όρος «κλίση» αναφέρεται στο μέτρο της μεταβολής όλων των βαρών ενός μοντέλου ως αποτέλεσμα της μεταβολής του σφάλματος. Μπορούμε επίσης να σκεφτούμε την κλίση ως την κλίση μιας συνάρτησης. Όσο μεγαλύτερη είναι η κλίση, τόσο πιο απότομη είναι η κάθοδος και τόσο γρηγορότερα μαθαίνει ένα μοντέλο. Αν όμως η κλίση είναι μηδενική, το μοντέλο σταματά να μαθαίνει. Μαθηματικά, η κλίση είναι μια μερική παράγωγος ως προς τις εισόδους της. Ένα απτό παράδειγμα είναι το εξής: Ένας τυφλός άνθρωπος θέλει να ανέβει στην κορυφή ενός λόφου με τον λιγότερο δυνατό αριθμό βημάτων. Αρχικά, μπορεί να αρχίσει να ανεβαίνει το λόφο κάνοντας πολύ μεγάλα βήματα προς την πιο απότομη κατεύθυνση, όσο δεν είναι κοντά στην κορυφή. Καθώς πλησιάζει όμως στην κορυφή, τα βήματά του γίνονται ολοένα και μικρότερα για να αποφύγει το να την υπερβεί. Αυτή η διαδικασία μπορεί να περιγραφεί μαθηματικά χρησιμοποιώντας την έννοια της κλίσης [1].
Η εξίσωση της μεθόδου
Η εξίσωση που περιγράφει τη μέθοδο είναι:
1. Pn+1: Αντιπροσωπεύει τη νέα θέση ή το νέο σύνολο παραμέτρων. Κατά την εκτέλεση της κλίσης καθόδου, η θέση ενημερώνεται βάσει της κατεύθυνσης και του ρυθμού εκμάθησης.
2. pn: Αντιπροσωπεύει την τρέχουσα θέση ή το τρέχον σύνολο παραμέτρων.
3. η: Ο ρυθμός εκμάθησης. Αυτή η παράμετρος καθορίζει πόσο μεγάλο είναι το βήμα προς την επόμενη θέση. Είναι σημαντικό να επιλεγεί με προσοχή, καθώς μικρές μεταβολές μπορούν να επηρεάσουν σημαντικά τον χρόνο και την ποιότητα της εκπαίδευσης.
4. ∇f(pn) Η κατεύθυνση της πιο απότομης κατάβασης της συνάρτησης κόστους στο σημείο pn.
Σε κάθε επανάληψη, η νέα θέση που προκύπτει είναι αντίστροφη προς την κατεύθυνση, ενώ το μέγεθος της ενημέρωσης ελέγχεται από τον ρυθμό εκμάθησης. Ο αλγόριθμος συνεχίζει να εκτελείται μέχρι να επιτευχθεί σύγκλιση σε ένα ολικό ελάχιστο. Αυτή η διαδικασία επιτρέπει στο μοντέλο να ενημερώνει τις παραμέτρους του προς την κατεύθυνση που μειώνει τη συνάρτηση κόστους, ελαχιστοποιώντας έτσι την απόκλιση και βελτιώνοντας την απόδοση του μοντέλου.
Εφαρμογές της μεθόδου
Η εφαρμογή της κλίσης καθόδου είναι ευρέως διαδεδομένη σε προβλήματα μηχανικής μάθησης.
1. Εκπαίδευση Νευρωνικών Δικτύων (Neural Networks):
Τα νευρωνικά δίκτυα χρησιμοποιούνται ευρέως σε προβλήματα μηχανικής μάθησης, όπως αναγνώριση εικόνας, φωνής, και άλλα. Κατά τη διάρκεια της εκπαίδευσης των νευρωνικών δικτύων, η κλίση καθόδου χρησιμοποιείται για την ενημέρωση των βαρών του δικτύου με σκοπό την ελαχιστοποίηση της συνάρτησης κόστους [2].
2. Γραμμική Κατηγοριοποίηση και Παλινδρόμηση: Σε αλγόριθμους παλινδρόμησης και κατηγοριοποίησης, όπως η γραμμική παλινδρόμηση και η λογιστική παλινδρόμηση, η κλίση καθόδου χρησιμοποιείται για την εκπαίδευση του μοντέλου προσαρμόζοντας τις παραμέτρους προς την κατεύθυνση της ελαχιστοποίησης του κόστους [3].
3. Μηχανή Διανυσματικής Υποστήριξης (SVM): Η κλίση καθόδου χρησιμοποιείται για την εκπαίδευση μοντέλων SVM προσαρμόζοντας τις παραμέτρους τους για την επίτευξη βέλτιστης απόστασης μεταξύ των κλάσεων [4].
4. Βελτιστοποίηση Υπερπαραμέτρων: Η κλίση καθόδου χρησιμοποιείται επίσης για τη βελτιστοποίηση των υπερπαραμέτρων μοντέλων μηχανικής μάθησης, όπως οι ρυθμίσεις του ρυθμού εκμάθησης [5].
Τύποι Κλίσης Καθόδου
Υπάρχουν τρία είδη αλγορίθμων κλίσης καθόδου:
Η στοχαστική κλίση καθόδου, ο Batch gradient descent και ο Mini-batch gradient descent
• Στοχαστική Κλίση Καθόδου (Stochastic Gradient Descent): Η στοχαστική κλίση καθόδου βασίζεται στην μεθοδολογία που αναφέρθηκε παραπάνω, με την διαφορά ότι η κλίση υπολογίζεται με βάση ενός υποσυνόλου του σετ δεδομένων. Η λειτουργία αυτή επιταχύνει σημαντικά τον αλγόριθμο καθιστώντας την απαραίτητη σε προβλήματα υψηλών διαστάσεων. Εκ πρώτης όψεως, η στοχαστική κλίση καθόδου παρουσιάζεται ως αλγόριθμος χαμηλής ποιότητας, ωστόσο επιλύονται σημαντικά προβλήματα του κλίσης καθόδου όπως είναι η προσκόλληση της συνάρτησης σε τοπικά ελάχιστα.
• Batch Gradient Descent: Ο batch gradient descent είναι ένας αλγόριθμος βελτιστοποίησης που χρησιμοποιείται για την εκπαίδευση μοντέλων στην μηχανική μάθηση. Λειτουργεί ως εξής:
1. Υπολογισμός Σφάλματος: Κάθε φορά που το μοντέλο μηχανικής μάθησης κάνει μια πρόβλεψη, υπολογίζουμε το πόσο λάθος ήταν σε σχέση με το πραγματικό αποτέλεσμα.
2. Σύνολο Εκπαίδευσης: Έχουμε ένα σύνολο εκπαίδευσης με πολλά παραδείγματα.
3. Μέσος Υπολογισμός: Ο Batch Gradient Descent υπολογίζει το συνολικό σφάλμα για όλα τα παραδείγματα εκπαίδευσης.
4. Ανανέωση Παραμέτρων: Με βάση αυτό το συνολικό σφάλμα, ανανεώνουμε τις παραμέτρους του μοντέλου μας.
5. Επανάληψη: Επαναλαμβάνουμε τη διαδικασία για πολλές εποχές (epochs), προσπαθώντας να μειώσουμε συνεχώς το σφάλμα.
• Mini-Batch Gradient Descent: Ο Mini-batch gradient descent συνδυάζει ιδέες από τους αλγορίθμους batch gradient descent και στοχαστικής κλίσης καθόδου. Διαιρεί τα σετ δεδομένων εκπαίδευσης σε μικρά τμήματα (μικρές δέσμες) και κάνει ενημερώσεις(updates) σε κάθε δέσμη. Αυτή η προσέγγιση εξασφαλίζει μια ισορροπία ανάμεσα στην αποτελεσματικότητα του batch gradient descent και την ταχύτητα της στοχαστικής κλίσης καθόδου [6].
Προκλήσεις
Τοπικά Ελάχιστα και Σημεία Σέλας
Σε προβλήματα όπου θέλουμε να βρούμε το καλύτερο αποτέλεσμα (γενικά το "ελάχιστο"), μπορεί να υπάρχουν τοπικά ελάχιστα. Αυτά είναι σημεία που μοιάζουν με ελάχιστα, αλλά δεν είναι το πραγματικό καλύτερο αποτέλεσμα. Υπάρχουν επίσης τα σημεία σέλας, σημεία δηλαδή όπου η καμπύλη της συνάρτησης είναι επίπεδη και μπορεί να είναι δύσκολο για τον αλγόριθμο να προχωρήσει προς μια κατεύθυνση. Κάτι που μπορεί να βοηθήσει τον αλγόριθμο να "δραπετεύσει" από τα τοπικά ελάχιστα και τα σημεία σέλας, επιτρέποντας του να συνεχίσει την εύρεση του γενικού ελαχίστου, είναι ο θόρυβος. Ο "θόρυβος" στην κλίση καθόδου αναφέρεται σε μικρές ανεπιθύμητες αλλαγές στην κατεύθυνση. Αυτό μπορεί να οφείλεται σε διάφορους παράγοντες, όπως τα δεδομένα που δεν είναι απόλυτα καθαρά.
Κατά την εκπαίδευση βαθιών νευρωνικών δικτύων (DNN), όπως τα αναδρομικά νευρωνικά δίκτυα (RNN), μπορεί να συναντήσουμε άλλους 2 τύπους προβλημάτων:
Vanishing gradients
Συμβαίνει όταν η κλίση γίνεται πολύ μικρή. Καθώς προχωράμε πίσω κατά τη διαδικασία του backpropagation, η κλίση συνεχίζει να μικραίνει, κάνοντας τα πρώτα επίπεδα του δικτύου να μαθαίνουν πιο αργά από τα επόμενα. Αυτό μπορεί να οδηγήσει σε ανανέωση των βαρών μέχρι να γίνουν αμελητέα (δηλαδή 0), με αποτέλεσμα να μην μαθαίνει πλέον το μοντέλο.
Exploding gradients
Συμβαίνει όταν η κλίση γίνεται πολύ μεγάλη, δημιουργώντας ένα ασταθές μοντέλο. Σε αυτήν την περίπτωση, τα βάρη του μοντέλου θα αυξηθούν πολύ, με αποτέλεσμα να γίνονται NaN (μη ορισμένα). Μια λύση σε αυτό το πρόβλημα είναι να χρησιμοποιηθεί μια τεχνική μείωσης των διαστάσεων, η οποία μπορεί να βοηθήσει στον περιορισμό της πολυπλοκότητας μέσα στο μοντέλο.
Αναφορές
[1] N. Donges, “Gradient Descent in Machine Learning: A Basic Introduction,” 2023. [Online]. Available: https://builtin.com/data-science/gradient-descent.
[2] E. M. Dogo, O. J. Afolabi, N. I. Nwulu, B. Twala, and C. O. Aigbavboa, “A comparative analysis of gradient descent-based optimization algorithms on convolutional neural networks,” in 2018 international conference on computational techniques, electronics and mechanical systems (CTEMS), 2018, pp. 92–99.
[3] J. Friedman and B. E. Popescu, “Gradient directed regularization for linear regression and classification,” Technical Report, Statistics Department, Stanford University, 2003.
[4] C.-J. Hsieh, K.-W. Chang, C.-J. Lin, S. S. Keerthi, and S. Sundararajan, “A dual coordinate descent method for large-scale linear SVM,” in Proceedings of the 25th international conference on Machine learning, 2008, pp. 408–415.
[5] D. Maclaurin, D. Duvenaud, and R. Adams, “Gradient-based hyperparameter optimization through reversible learning,” in International conference on machine learning, 2015, pp. 2113–2122.
[6] IBM, “What is gradient descent?,” 2023. [Online]. Available: https://www.ibm.com/topics/gradient-descent.