Η Μέθοδος Dropout
Από RemoteSensing Wiki
| Γραμμή 1: | Γραμμή 1: | ||
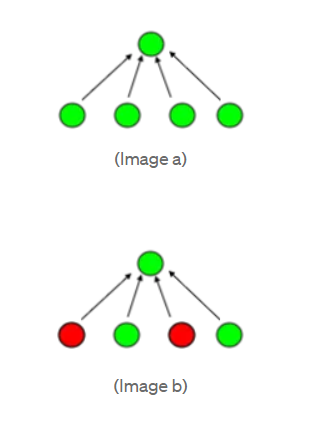
| - | [[εικόνα: dropout layers.png|thumb|right|400px|'''Εικόνα 1:''' Layer νευρωνικού δικτύου πριν και μετά την εφαρμογή της μεθόδου Dropout [1 | + | [[εικόνα: dropout layers.png|thumb|right|400px|'''Εικόνα 1:''' Layer νευρωνικού δικτύου πριν και μετά την εφαρμογή της μεθόδου Dropout [1]]] |
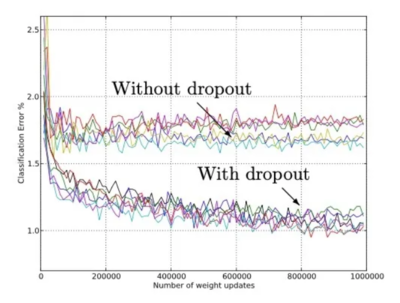
| - | [[εικόνα: paradeigma_dropout.png|thumb|right|400px|'''Εικόνα 2:''' Μείωση των σφαλμάτων της ταξινόμησης μετά την εφαρμογή της μεθόδου Dropout[1 | + | [[εικόνα: paradeigma_dropout.png|thumb|right|400px|'''Εικόνα 2:''' Μείωση των σφαλμάτων της ταξινόμησης μετά την εφαρμογή της μεθόδου Dropout[1]]] |
[[εικόνα: pseydokwdikas.png|thumb|right|400px|'''Εικόνα 3''' ]] | [[εικόνα: pseydokwdikas.png|thumb|right|400px|'''Εικόνα 3''' ]] | ||
[[εικόνα: neyronika_diktia_.png|thumb|right|400px|'''Εικόνα 4:''' Εικονική αναπαράσταση ενός νευρωνικού δικτύου]] | [[εικόνα: neyronika_diktia_.png|thumb|right|400px|'''Εικόνα 4:''' Εικονική αναπαράσταση ενός νευρωνικού δικτύου]] | ||
| - | |||
'''<span style="color:#006400"> Τι είναι; </span>''' | '''<span style="color:#006400"> Τι είναι; </span>''' | ||
Παρούσα αναθεώρηση της 10:05, 31 Ιανουαρίου 2024
Τι είναι;
Η μέθοδος Dropout είναι μια μέθοδος κανονικοποίησης που χρησιμοποιείται κυρίως στην εκπαίδευση των νευρωνικών δικτύων προκειμένου να λυθεί το πρόβλημα του overfitting. Είναι μια ισχυρή τεχνική που ενώ σχετίζεται κυρίως με νευρωνικά δίκτυα, οι αρχές της μπορούν να προσαρμοστούν και σε άλλους στατιστικούς αλγόριθμους, πχ σε ensemble μεθόδους όπως είναι η random forests και η gradient boosting, σε γραμμική και λογιστική παλινδρόμηση, σε αλγορίθμους ημι-εποπτευόμενης μάθησης και πολλούς άλλους.
Τι είναι το overfitting;
To overfitting είναι μια κατάσταση που συμβαίνει όταν ένα νευρωνικό δίκτυο εκπαιδεύεται τόσο πολύ στα δεδομένα εκπαίδευσης, που αρχίζει να μαθαίνει τα δεδομένα αυτά τόσο καλά, που χάνει την δυνατότητα να γενικεύει όταν λάβει νέα δεδομένα. Αυτό συμβαίνει συχνότερα όταν περίπλοκα νευρωνικά δίκτυα εκπαιδεύονται πάνω σε σχετικά μικρό σετ δεδομένων. Για παράδειγμα, είναι σαν ένα άτομο να διαβάζει και να μαθαίνει πολύ καλά ένα συγκεκριμένο βιβλίο μιας θεματικής ενότητας και να είναι σε θέση να απαντήσει ανασύροντας από τη μνήμη του οποιαδήποτε πληροφορία έχει να κάνει με το συγκεκριμένο βιβλίο, αλλά αν ερωτηθεί κάτι που ναι μεν αφορά στη θεματική ενότητα του βιβλίου αλλά διαφοροποιείται από αυτό, αδυνατεί να απαντήσει ή απαντά λανθασμένα. Ας δούμε δύο απλά παραδείγματα.
o Έστω ότι εκπαιδεύουμε ένα νευρωνικό δίκτυο για να μπορεί να αναγνωρίζει αν ένα αντικείμενο είναι γάτα ή όχι από εικόνες, και έστω ότι για την εκπαίδευσή του χρησιμοποιούμε ένα σύνολο εικόνων που λαμβάνει υπόψη διάφορες γωνίες λήψης, φωτεινότητα και το φόντο άλλα μόνο μια μικρή ποικιλία από ράτσες γάτας. Το δίκτυο θα αναπτύξει περίπλοκους κανόνες ώστε να είναι σε θέση να αναγνωρίσει τις συγκεκριμένες ράτσες μέσω του σετ δεδομένων, ωστόσο αν δοκιμάσουμε το δίκτυο με φωτογραφίες γατών που διαφέρουν σημαντικά από τις ράτσες του σετ, υπάρχει μεγάλη πιθανότητα να μην είναι αποτελεσματικό. Αυτό οφείλεται στο γεγονός ότι το δίκτυο έχει "μάθει" πολύ συγκεκριμένα χαρακτηριστικά από το σύνολο δεδομένων εκπαίδευσης, αλλά δεν έχει αναπτύξει τη γενικότητα για να αντιμετωπίσει νέες, διαφορετικές καταστάσεις.
o Έστω ότι εκπαιδεύουμε τώρα ένα νευρωνικό δίκτυο έτσι ώστε να είναι σε θέση να διαχωρίζει τα “spam” email από τα υπόλοιπα και έστω ότι για να το εκπαιδεύσουμε χρησιμοποιούμε παραδείγματα από διάφορα “spam” email. Το δίκτυο είναι πιθανό να υπερεκπαιδευτεί και να αναγνωρίζει ως “spam” μόνο όσα mail περιέχουν κάποιες συγκεκριμένες λέξεις ή συγκεκριμένο τρόπο γραφής. Το αποτέλεσμα θα είναι να μην αναγνωρίζει ως “spam” mail που δεν περιέχουν αυτές τις λέξεις καθώς όμως μπορεί να συμβεί και το αντίθετο, δηλαδή mail που δεν είναι “spam” να ταξινομούνται ως τέτοια.
Πώς αντιμετωπίζεται το overfitting;
• Έχουν αναπτυχθεί αρκετές μέθοδοι και αλγόριθμοί προκειμένου να λυθεί το πρόβλημα το overfitting. Οι περισσότερες και πιο παραδοσιακές από αυτές αφορούν κυρίως γραμμικά νευρωνικά δίκτυα. Μερικά παραδείγματα είναι η L1 Regularization, η L2 Regularization, η Elastic Net και η Early Stopping που εφαρμόζονται κυρίως σε γραμμικά νευρωνικά δίκτυα.
Όπως αναφέραμε και πριν η μέθοδος Dropout είναι μια μέθοδος κανονικοποίησης που χρησιμοποιείται στην εκπαίδευση των νευρωνικών δικτύων προκειμένου να λυθεί το πρόβλημα του overfitting. Το βασικό της πλεονέκτημα σε σχέση με τις υπόλοιπες μεθόδους κανονικοποίησης που αναφέραμε πριν είναι ότι μπορεί να εφαρμοστεί και σε μη γραμμικά μοντέλα. Η βασική ιδέα πίσω από το Dropout είναι ότι “απενεργοποιεί” τυχαία κάποιους νευρώνες σε κάθε επανάληψη εκπαίδευσης. Αυτό σημαίνει ότι κάθε φορά το δίκτυο μαθαίνει να εκπαιδεύεται βασιζόμενο σε διαφορετικούς συνδυασμούς νευρώνων γεγονός που επιλύει το πρόβλημα του overfitting αφού οι νευρώνες “μαθαίνουν” να μην εξαρτώνται υπερβολικά ο ένας από τον άλλον. Ας την δούμε όμως πιο αναλυτικά. Για να εφαρμοστεί η μέθοδος Dropout ορίζεται η υπερπαράμετρος p (hyperparameter p ή dropout p ) η οποία αναφέρεται στο ποσοστό των νευρώνων που “απενεργοποιούνται” κατά τη διάρκεια της εκπαίδευσης. Ουσιαστικά η p είναι η πιθανότητα ένας νευρώνας να είναι ενεργοποιημένος η απενεργοποιημένος κατά τη διάρκεια της εκπαίδευσης. Οι τιμές που μπορεί να πάρει η p είναι από 0 έως 1 αλλά συνήθως ορίζεται από 0.2-0.5. Για κάθε επανάληψη εκπαίδευσης ορίζεται διαφορετική υπερπαράμετρος. Κατά την απενεργοποίηση ενός νευρώνα η τιμή της εξόδου του τίθεται ως μηδέν και δεν συμμετέχει στην καθόλου στην διαμόρφωση της τελικής εξόδου του μοντέλου. Σε κάθε επανάληψη εκπαίδευσης ορίζεται μια διαφορετική τιμή p και στο τέλος γίνεται ένας συνδυασμός των βασικών διεργασιών κάθε εκπαίδευσης προκειμένου να έχουμε την τελική ολοκληρωμένη εκπαίδευση του δικτύου. Σε κάθε layer τα βάρη του κάθε νευρώνα κατανέμονται ανάλογα με τον αριθμό τους. Στην Εικόνα 1a φαίνεται ένα layer που αποτελείται από 4 νευρώνες. Το βάρος κάθε νευρώνα θα είναι ¼=0.25. Έστω τώρα ότι εφαρμόζουμε την μέθοδο dropout σε αυτό το layer εικόνα 2b. Τότε θα μείνουν δύο νευρώνες και το βάρος στον κάθε ένα θα είναι ½=0.5. Όμως επειδή δεν θέλουμε τα βάρη στη διαδικασία της εκπαίδευσης να είναι τόσο υψηλά, παρά μόνο να εκπαιδεύσουμε το δίκτυο να μπορεί κάθε φορά να λειτουργεί χωρίς να εξαρτάται από συγκεκριμένους νευρώνες, πολλαπλασιάζουμε με p τα βάρη των νευρώνων που έχουν μέινει και το αποτέλεσμα είναι ότι έχουμε πάλι βάρος 0.25 για τους δύο νευρώνες που έχουν μείνει. Αυτή είναι και η βασική μεθοδολογία που ακολουθείται κάθε φορά με διάφορες προσαρμογές της πιθανότητας p.
Υπάρχουν αρνητικά της μεθόδου;
Ενώ η μέθοδος dropout έχει βοηθήσει κατά πολύ στην βελτίωση του overfitting έχει και ορισμένα αρνητικά. Τα βασικότερα από αυτά είναι: Ενώ η μέθοδος dropout παραμένει ένα ισχυρό εργαλείο για την αντιμετώπιση της υπερεκπαίδευσης και της βελτίωσης της γενίκευσης σε πολλά προβλήματα μηχανικής μάθησης, η βέλτιστη χρήση της εξαρτάται από τα χαρακτηριστικά του συγκεκριμένου προβλήματος και του μοντέλου που χρησιμοποιείται. Μερικά από τα βασικότερα και συχνότερα προβλήματα που μπορεί να παρουσιαστούν είναι:
1. Χρειάζεται αρκετά παραπάνω χρόνο να εκπαιδευτεί.
2. Υπάρχει κίνδυνος απώλειας πληροφορίες κατά την απενεργοποίηση νευρώνων.
3. Τα νευρωνικά δίκτυα παρουσιάζουν μεγάλη ευαισθησία στην επιλογή της τιμής p. Μπορούν πολύ εύκολα να υποεκπαιδευτούν αν οριστεί μια λανθασμένη τιμή p
4. Είναι δύσκολη η εφαρμογή της σε συγκεκριμένες αρχιτεκτονικές δικτύου όπως είναι για παράδειγμα τα συνελικτικά νευρωνικά δίκτυα (convolutional neural networks)
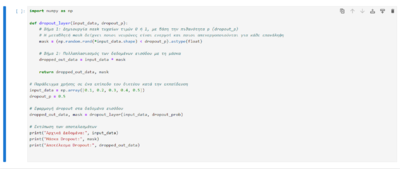
Στην Εικόνα 3 Παρακάτω βλέπουμε ένα παράδειγμα απλού κώδικα που δείχνει πώς θα μπορούσε να εφαρμοστεί η μέθοδος Dropout κατά την εκπαίδευση σε γλώσσα προγραμματισμού python.
Λίγα Λόγια για τα Νευρωνικά Δίκτυα
Τα νευρωνικά δίκτυα είναι υπολογιστικά συστήματα που ουσιαστικά “αντιγράφουν” τον τρόπο που λειτουργεί ο ανθρώπινος εγκέφαλος. Αποτελούνται από μια σειρά “τεχνιτών νευρώνων” που συνδέονται μεταξύ τους με διάφορους τρόπους προκειμένου να επεξεργαστούν πληροφορίες.
Μπορούμε να χωρίσουμε τον τρόπο που λειτουργεί ένας τεχνητός νευρώνας σε 5 βασικά βήματα (Εικόνα 4):
1. Είσοδος (Input): Κάθε νευρώνας δέχεται μια είσοδο που μπορεί να είναι το αποτέλεσμα μιας μέτρησης ή η έξοδος ενός άλλου νευρώνα
2. Κάθε είσοδος χαρακτηρίζεται από ένα βάρος (weight). Το βάρος καθορίζει πόση σημασία θα δοθεί στην αντίστοιχη είσοδο.
3. Επεξεργασία (Processing): κάθε νευρώνας επεξεργάζεται την είσοδο πολλαπλασιάζοντας την με το αντίστοιχο βάρος.
4. Σύνοψη (Summation): το άθροισμα των πολλαπλασιασμών συνοψίζεται για να δώσει ένα συνολικό αποτέλεσμα
5. Συνάρτηση ενεργοποίησης και έξοδος (Activation Function and Output): το τελικό αποτέλεσμα περνά μέσα από μια συνάρτηση ενεργοποίησης που με βάσει το αποτέλεσμα θα ορίσει αν θα πραγματοποιήσει έξοδο ή όχι.
Τα νευρωνικά δίκτυα αποτελούνται από πολλούς τέτοιους νευρώνες οι οποίοι είναι οργανωμένοι σε στρώματα (layers), και ο κάθε ένας από αυτούς εκτελεί την παραπάνω σειρά ενεργειών. Τα layers εκτός από αυτά της είσοδού και της εξόδου ονομάζονται “κρυφά” καθώς δεν υπάρχει η δυνατότητα από κάποιον εξωτερικό παρατηρητή να βλέπει ακριβώς τις διεργασίες που λαμβάνουν χώρα εκεί.
Κάποια παραδείγματα εφαρμογών στα οποία χρησιμοποιούνται τα νευρωνικά δίκτυα είναι η αναγνώριση εικόνων, η αυτόματη μετάφραση, η φωνητική αναγνώριση καθώς και τα συστήματα συστάσεων σε πλατφόρμες όπως είναι οι ειδήσεις του Google και οι αλγόριθμοι του Facebook του Instagram κτλ.
Βιβλιογραφία
[1] S. ’Nitish, H. ’Geoffrey, K. ’Alex, S. ’Ilya, and S. ’Ruslan, “Dropout: A Simple Way to Prevent Neural Networks from Overfitting,” Journal of Machine Learning Research, pp. 1929–1958, 2014.